P6 alludes to a
NYT article about studies on self-reporting of sexual partners. It's extremely common for studies of this type to report that "men have
x partners, women have
y partners," where
x >>
y. This is mathematically impossible, which I would think should be obvious. I've heard this sort of statistic repeated
ad nauseum, and I've long accepted its unchallenged acceptance as more proof that people either hear evidence of their irrational prejudices, or they tune out and get indignant.
The Myth, the Math, the Sex (Gina Kolata): Everyone knows men are promiscuous by nature. It’s part of the genetic strategy that evolved to help men spread their genes far and wide. The strategy is different for a woman, who has to go through so much just to have a baby and then nurture it. She is genetically programmed to want just one man who will stick with her and help raise their children.
Surveys bear this out. In study after study and in country after country, men report more, often many more, sexual partners than women.
One survey, recently reported by the federal government, concluded that men had a median of seven female sex partners. Women had a median of four male sex partners. Another study, by British researchers, stated that men had 12.7 heterosexual partners in their lifetimes and women had 6.5.
Well, this is impossible. Moreover, forget about prostitution: it holds even in countries where laws against prostitution are not only strictly enforced, but also where prostitution is actually not tenable. But try telling that to commentator "Solar Soul":
It's not mathematically impossible for women to be less promiscuous than men. You just need a small pool of promiscuous women sleeping with a larger pool of promiscuous men. If five promiscuous girls at your high school slept with twenty promiscuous guys, out of a population of 100 guys and 100 girls, then 5% of the girls would be promiscuous, and 20% of the guys would be promiscuous. Sometimes, I really wonder what a PhD is worth.
First, the response is clearly guided by irritation: "I may not know anything about math, but I know women are chaste and men are sex-glutted scumbags." Second, in the example, provided (the high school), Solar Soul is comparing the incidence of arbitrarily-defined "promiscuous ones" in the population of 100 men and 100 women. The example would work slightly better, incidentally, if it used 15 "promiscuous girls" and 60 "promiscuous guys" since at least that way, a majority of the men are "promiscuous" and the majority of women still aren't. It's still far of the mark, though, because the average number of partners is the same for both sexes... which is what the NYT article is all about. It's erroneous to compare
modes to modes unless the mode is what you care about, which isn't the case here.
Let's turn now to a (perhaps excessively) serious discussion of the matter:
Norman Brown: If surveys elicit accurate reports from their respondents, heterosexual men and women should, on average, report having had the same number of partners. This is because each new SP for a man is also a new SP for a woman. Thus, for a closed population, men and women must have the same number of opposite-sex SPs, and therefore should generate similar reports. This, however, is rarely the case. Instead, men typically report two to four times as many opposite-sex partners as women.
Wiederman: Rather than a small but statistically significant gender difference, the typical discrepancy in men's and women's lifetime number of sex partners is large by any definition. For example, in national samples, the mean number of sex partners for men and women, respectively, was 12.3 versus 3.3 in the United States (Smith, 1991), 9.9 versus 3.4 in Britain (Wellings et al., 1994), 11.0 versus 3.3 in France (ACSF, 1992), 10.2 versus 4.2 in New Zealand (Davis et al., 1993), and 12.5 versus 5.2 in Norway (Sundet et al., 1989). In populations that are more or less closed systems with an approximately equal ratio of men and women, such as the United States (U.S. Bureau of the Census, 1993), this apparent gender discrepancy does not make logical sense (Einon, 1994; Gurman, 1989).
The operant term here is probably "closed." In some cases, such studies do specify that the respondents are talking about heterosexual contacts; even if they weren't, we'd have to wonder about the conjecture that the massive disparity came from
uniquely male homosexuality. More significantly, especially in dense urban areas, it's reasonable to conjecture that numbers of partners are statistically concentrated (like net assets). Put another way, the great majority of people anywhere have 0-2 partners in any given 12-month period, and 1-3 partners in any given five-year period. But it's possible to have a group of, say, 1% of women (sex workers) who are seldom or never surveyed, who account for the greater part of all female sexual encounters; and another group of, say, 10% of men, who have far fewer encounters than the female sex workers, but vastly more than the remaining 90% of men. These 10% would certainly be sufficiently numerous to be represented, even realistically, by a survey like the CDC's; but their partners would be statistically invisible.
This might be true. Weiderman is doubtful, based on Einon's research:
Hypersexual women and prostitutes. Several authors [] have proposed that perhaps the apparent gender discrepancy in number of sex partners is explained by existence of a small subgroup of women who have had sex with an enormous number of men. To address this possibility of a subgroup of highly experienced women who were not prostitutes, Einon (1994) analyzed data from the national samples collected in Britain [] and France [] She found no evidence for the notion that there are more atypically "hypersexual" women compared to such men (and actually found evidence for a relatively greater incidence of "hypersexual" men who reported extremely large numbers of sex partners).
What about professional prostitutes? These women presumably have large numbers of male sex partners, yet may be less likely to be included in studies using typical sampling methodology. Einon (1994) also calculated the number of different male clients that prostitutes in Britain would need to service to resolve the gender discrepancy in self-reported lifetime number of sex partners in that country.
But
Brewer, et. al. (2000) contradict this finding:
Brewer, et al.: Einon (18) addressed and dismissed the prostitution explanation for the discrepancy in the British household survey (5). However, her analysis of the lifetime number of reported partners is undermined by the use of point and annual, rather than lifetime, prevalences of prostitutes, and thus does not adjust for the cumulative number of partners that all prostitutes from multiple cohorts had over respondents' lifetimes.
[...]
After adjusting for these prostitution-related factors, the ratios for the sex discrepancy in the reported number of sexual partners hover slightly above and below 1 [] indicating that prostitution can account for essentially all of the disparity.
Weiderman examines some other possible explanations in his '97 article.
Several authors have noted that, compared to women, men tend to select sex partners who are relatively younger and such a gender difference in partner choice may affect self-reported lifetime number of sex partners... In other words, as most surveys involve adult respondents (age 18 years and older), some men included in the sample have had sex with female partners who are not old enough to be included in the survey. Although this fact may explain some small degree of the gender discrepancy, it cannot explain adequately the relatively large difference between men's and women's self-reports. That is, in national surveys, men typically report approximately three times as many lifetime sex partners as do women... Preference for pre-adult sex partners explains the apparent gender discrepancy in lifetime partners only if two thirds of adult men's partners are currently younger than age 18, which is a highly unlikely scenario...
Similarly, it would seem that if men begin their sexual careers earlier than do women, men would have a longer period of time in which to accumulate sex partners. However, any such difference in onset of sexual intercourse does not explain the gender discrepancy in lifetime number of sex partners because men still have to have a female partner, regardless of the age of the male. Additionally, at least among the most recent generation of young adults, there does not appear to be a gender discrepancy in age at first experience of sexual intercourse.
In fact, according to the
CDC report (PDF), distribution of sexual partners in the 15-19% cohort is almost identical for each partner count; this would contradict the principle that young boys would be more likely to exaggerate their sexual experiences than older men. We'll see how this works out later, because it turns out they still do (just not on purpose).
Brewer, et. al. (2000) actually suggest that, far from exaggerating sexual conquests, men do not report contact with prostitutes when responding to surveys.
In two different parts of the Colorado Springs interview, heterosexual men were asked about contact with prostitutes in the last 5 years, with the second question referring to prostitutes in Colorado Springs only. Eleven of the 110 clients acknowledged prostitute partners only in response to the second question, and 2 additional men who did not report contact with prostitutes were known to be clients from prostitutes' naming them specifically as clients in another part of the interview.
However, it could be argued that Brewer,
et al., in their enthusiasm at cracking the case, simply widened the gap: if the female sex-workers, representing 0.023% of the human population (of Colorado Springs, but they say that's representative) account for the entire difference,
and men are reluctant to report contacts with prostitutes on surveys, then it's possible that they merely uncovered a huge cesspool of underreported sexual activity involving men and prostitutes.
(Actually, they imply that they can explain pretty much any discrepancy that could have been found with prostitutes. It's like "
What Stumped the Bluejays." Since it could explain nearly any number you threw at them, I tend to suspect their study for that very reason. The other problem is, the study is mainly interested in establishing that (a) prostitutes account for a staggering volume of sex, and (b) men are reluctant to tell researchers that their impressive sexual CV's are padded with alleyway tricks. If that were true, however, it seems unlikely that this would have escaped the attention of so many different researchers with different methodologies.)
In any event, much of the discrepancy does indeed apply to a small number of men with large numbers of partners. Just as with income distribution at
the high end, distribution of sexual partners doesn't follow a normal distribution; if it did, long lifetimes of celibacy or people like
Bertrand Morane would appear once in a billion; in reality, they are quite common. Moreover, for women, large numbers of male partners tends to blur the gender division; according to the CDC study (p.12b), 32% of women with a lifetime count of ≥15 men had had same-sex encounters as well. For men, this tended to follow the plausible pattern of older men reporting more partners; only the >40 set had a >33% likelihood of reporting >15 partners (table 10). For women, only one ninth reached that level, but they did so earlier (25-29; see table 11); and after that age, the number slightly declined (!), suggesting that older cohorts of women offset their longer careers with a lower rate of new partners. The impression one gets examining table 11 is that a steady proportion of the respondents (20%) were adamant about having only one partner their entire lives—consistent with defining
female religious narratives.
At last, we return to my preferred explanation: the unintentional classification scheme.
Norman Brown: It is well established that people use multiple strategies to generate numerical estimates, that different strategies are associated with explicable characteristic biases, and that strategy use is influenced by the availability of task-relevant information and the actual magnitude of the to-be-estimated quantity [] Of particular relevance, Brown (1995, 1997) demonstrated that people asked to estimate event frequencies sometimes retrieve and count event instances (i.e., enumerate) and sometimes produce rapid intuitive estimates (i.e., rough approximations). Participants who enumerate often underestimate event frequencies because relevant instances may be permanently forgotten, because output interference causes some instances to become temporally inaccessible, and because people sometimes terminate their retrieval efforts before all relevant instances have been recalled. In contrast, participants who produce rough approximations often overestimate event frequencies. It is believed that people generate these estimates by mapping vague quantifiers (e.g., terms like "quite a few," "lots") onto a numerical response scale and that this process produces overestimation because the lower bound of the response scale is anchored but the upper bound is not (Brown, 1995).
It is conceivable that some people enumerate when reporting their number of lifetime SPs and others respond with rough approximations. If so, all else being equal, people who enumerate should produce smaller estimates than people who use rough approximations. Thus, if we assume that the mean number of SPs is the same for men and women and that men and women respond in good faith, then we should find that men rely more on strategies associated with larger estimates (e.g., rough approximation) and women rely more on those associated with smaller estimates (e.g., enumeration). If this is the case, then differential strategy use can explain the sex difference in reports of lifetime SPs.
P6 was skeptical and hooted a little at this
explanation:
How is this...Some strategies...are associated with relatively large reports, others...are associated with relatively small reports, and that men are more likely to use the former whereas women are more likely to use the latter.
Any different that this?P6: I think men lie about how many and women lie about how few.
The difference is that men use different methods ("strategies") of answering the question than women do, since women actually enumerate and men estimate. Bear in mind that I have no idea, since my lifetime total is pretty unambiguously fixed in my mind. Brown estimated that, when asked about totals during the preceding 12 months, gender discrepancies would disappear (which they certainly did).
An examination of the written protocols revealed that participants used several different strategies to generate their SP reports.(6) The most common of these was enumeration (e.g., "Counted all the names I remembered."); collapsing across sex, 39% of the sexually-active participants stated that they arrived at their estimates by recalling each of their partners. 29% used a tally-retrieval strategy. These people indicated that they maintain a tally in memory and that they responded to the lifetime question by recalling and stating the current value of this tally (e.g., "I kept track in my diary, and I know that my boyfriend is #27."). Another 17% indicated that their estimates were rough approximations. Protocols were assigned to this category when participants indicated that they generated their responses without carefully examining the available evidence. Such estimates were often accompanied by an expression of uncertainty (e.g., "Rough guess, give or take 1 or 2 partners"). In addition to these common strategies, 11% of the participants produced protocols that were too vague to be coded (e.g., "Memory") or that included only irrelevant information, 2% used a rate-based strategy (e.g., "Avg of 5/year from 16-21, then remained monogamous."), and 1% failed to respond.
[...]
In contrast to the lifetime estimates, the past-year SP estimates provided by the sexually active men (M = 3.45) were not significantly larger than those provided by the sexually active women (M = 2.58), t(173) = 1.26, ns. This replicates a common finding in the survey literature (ACSF Investigators, 1992; Johnson et al., 1992; Laumann et al., 1994; Morris, 1993; Smith, 1992) and has two important implications. First, the past-year data argue against the possibility that the sex difference reported above arose because our participants were responding in bad faith; if they had been, there should have been a reliable sex difference for both lifetime and past-year estimates. The past-year data also address an alternative explanation for the partner discrepancy reported above. One could argue that the men in our sample were actually more experienced than the women, and that the reported difference in estimated life-time SPs merely reflected this fact. However, given that the male and female participants were about the same age, and assuming that the men in this sample had more partners than the women, a sex difference should have been apparent in the past-year estimates as well as the lifetime estimates. Because the data do not support this prediction, we conclude that it is unlikely that men and women were drawn from qualitatively different samples.
And that's the difference.
NOTES:
mode: in statistics, the mode is the value that appears most commonly in the set. So, for example, if you have 100 people, and 10 of those people have had >10 sexual partners each, while the remaining 90 have had anywhere from 1 to 10 evenly distributed, then you would have 9 with one, 9 with 2,... 9 with 10, and the mode would be >10 since there are 10 with more than ten. You might even be incited to remark, "The group generally has more than partners each," which would convey a very erroneous impression even if >10 is the most common number of partners.
In the example cited, the mode is >4; if there were 60 "promiscuous" men & 15 "promiscuous" women, then the mode for the men would be >4, while that for the women would be 0. In Solar Soul's original version, the mode for both is 0.
Female religious narratives: coming from an evangelical protestant background, I have a fairly large amount of experience with testimonies by women and men about their religious epiphanies. It's relatively common for men to regale me with speeches about
their past, raunchy life; sometimes they exaggerate, as I was sometimes encouraged to do. I can't lie convincingly, so I just opted out. The man typically describes a life ridden with sex and drugs, with something goofy thrown in (video games come to mind), then talks about being saved by God and united with his doting wife. Perhaps it was just me, but I would always read a certain humiliation in the wife's blissful smile; she was the healthy salad with rice crackers, not the slab of steak and baked potato skins with the English pint of ale.
In contrast, the women had a narrative that was very long on descriptions of mental states, and short on a backstory of actual, you know,
sin. I use my mother as a canonical example: she would refer to a period of utter moral degeneration. When I was younger, I tried to get some clues about what cosmic depths of Dennis-Hopperesque depravity she'd sunk to. After one especially purple session, she finally spilled the beans: sometimes she didn't tithe. I would like to have seen the look on my face when she said that. Since that time, I've noticed that such defining religious narratives, for women, are rigidly and scrupulously confined to what is a matter of public record.
READING & SOURCES: William D. Mosher, Anjani Chandra, & Jo Jones , "
Sexual Behavior and Selected Health Measures: Men and Women 15–44 Years of Age, United States" (PDF-2005); Brewer,
et al., "
Prostitution and the sex discrepancy in reported number of sexual partners," The National Academy of Sciences (2000); Norman Brown, "
Estimating Number of Lifetime Sexual Partners"
Journal of Sex Research (1999); Michael W. Wiederman, "
The truth must be in here somewhere"
Journal of Sex Research (1997)
Jeff Grabmeier RE: research of Terri Fisher, "
Women's sexual behaviors may be closer to men's than previously thought," Ohio State Research (2003):
This article was designed to test the variance in women's and men's reporting of sexual experience under different interview regimes; generally, women were more susceptible to social pressures and context, whereas men tended to report the same thing regardless. One implication is that women tended to report larger numbers of sexual partners if they were likely to believe they were being tested for truthfulness on a polygraph. The implication is that the discrepancy reflects embarrassment about large numbers of partners, which shrinks as the embarrassment of being thought a slut is replaced by the embarrassment of being caught lying. Labels: anthropology, social research, statistics
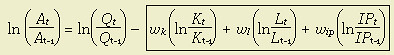
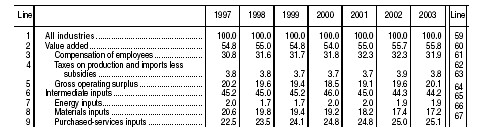
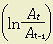is the annual increase in total factor productivity;
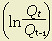is the annual increment in output;
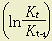is the annual increment in capital inputs;
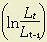is the annual increment in labor inputs;
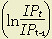is the annual increment in energy, materials, and business services.
