Dynamic General Equilibrium

The dynamic general equilibrium (DGE) model of economic behavior is the one that has prevailed in public policy analysis for about 30 years now. In its early form, it tended to use, and was known as, the "rational expectations hypothesis" (REH) ; and a money-neutral version of the business cycle, or "real business cycle" (RBC) theory. In the years since, there has been a shift of emphasis away from REH and RBC, towards the design of the model itself (DGE). Hence, DGE methodology can specifically exclude some of the early assumptions, and incorporate their converse.

When students are introduced to the concept of equilibrium, what they are are shown is the intersecting schedules of supply and demand. A leftward shift in the supply curve—perhaps due to the depletion of a particular input—causes the price to rise and the quantity demanded to decrease. A rightward shift in the demand curve—perhaps due to a change in fashion—also causes prices to increase, but also causes the quantity demanded to increase too.


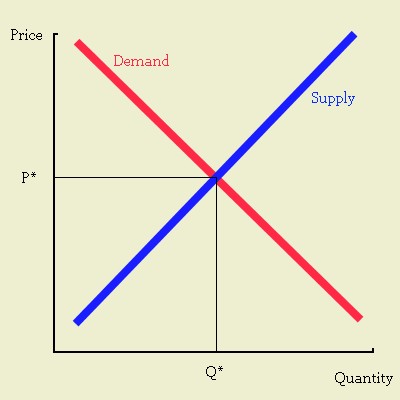
This is known as a partial equilibrium, since only a part of the determinants of the equilibrium are being looked at. In fact, professors are obligated to remind students that these conditions hold, "all other things being equal." If the supply curve moves to the right, we don't consider a sudden decrease in income, or a sudden shift rightward in the supply curves of other commodities.

Initially, the concept of general equilibrium appears to have been developed by Leon Walras (1870), and subsequently refined by Gustav Cassel (1918). Walras' original version did not fare well, but in the 1950's was revived by Kenneth Arrow and Gerard Debreu, and since then general equilibrium has evolved to become the essential governing idea of economic research.

In general equilibrium, all of the determinants of economic equilibrium are considered at once. This can be gone though a system of linear equations. The equations incorporate the utility functions of representative consumers, prior endowments of capital and labor, production functions (i.e., equations that provide the maximum output of commodities for an economy, given available labor and capital; see Egwald), and so on. The object is to create a mathematical representation of how an economy works.

Why?
Part of the reason is to examine the more complicated results of external change. For example, in intermediate microeconomics, students are typically introduced to indifference curves and budget lines. This allows students to analyze the difference between the income effect and the substitution effect (both of which involve changes in demand caused by changes in price). But the curves in the textbooks are usually drawn arbitrarily, to make a particular point; Marshallian general equilibrium theory tended to resist integrating all of the elements of Neoclassical (Marginalist) theory into a formal, mathematical model.

Colander: Why did Marshall focus his analysis on partial equilibrium and not formally develop his conception of general equilibrium? [...] I think it is correct that he felt incapable of specifying a meaningful formal general equilibrium system, [...] because he demanded intuitive correspondence between math and his understanding of the economy. [...]

Marshall's recognition of the analytic intractability of the general equilibrium problem, given the math available to him, and his desire for concreteness in his economics, led him to shy away from abstract specifications of general equilibrium.

However, the work of Arrow and Debreu was to effectively synthesize the views of Marshall with Walras' (inter alia) notions of general equilibrium. In other words, Marshall's partial, "cross sections" of economic relations (like the indifference curve) are expanded into the additional dimensions required to allow for a formal, unique equilibrium for any given vector of determinant variables—capital and labor endowments, consumer preferences, technology (production functions) and so on.

A word on simplification: in order to represent something as complex as an entire economy with a series of linear equations, economists typically rely on a principle known as positive economics. Positive economics, in its most reduced form, merely asks that economic analysis be judged on the basis of its accuracy of predictions, rather than normative (value) judgments. An interesting corollary to this is that we are advised to consider an economic theory on the basis of its predictive performance, rather than the realism of its assumptions[*]. Hence, we might assume that the US economy consists of 300 million identical actors, rather than people varying widely in income, ability, or preferences. We might ignore the role of monopolies, or involuntary unemployment, or ignorance about the relevant policy preferences of monetary authorities, and that's all right, if the result provides a reasonably accurate or useful prediction of the future.

Variations on a Theme
As mentioned above, DGE theory initially incorporated mathematical equations that "assumed" no liquidity constraints, rational expectations hypothesis (REH), and real business cycles (RBC). Initially, REH was considered to be identical to DGE, which is why you find all of the DGE ideas expressed in The Rational Expectations Revolution (cited below); Preston Miller's book wasn't entitled The Dynamic General Equilibrium Revolution, although six years later it might well have been: since 2001, usage of the term has sharply diminished.

Moreover, there are different systems of equations that may be used. The most common are those of the Ramsey-Cass-Koopmans model: the closed economy consists of a household with an exogenous labor supply over time. One good is produced in each period using inputs of labor and capital, and output in each period can be either consumed or invested. There is perfect competition in all markets and no taxes. Individuals are assumed to have an infinite horizon, and expectations by private agents are forward-looking and rational. Hence, all agents have perfect foresight because there is no uncertainty. These assumptions imply that the allocation of resources by a central planner who maximizes the utility of the representative agent is identical to the allocation of resources in an undistorted decentralized economy.

The dynamic component comes from the use of mathematical models to simulate the behavior of such an economy over time (an innovation of Edward C. Prescott's "Time to Build" paper, cited below). In such a model, the economy has predictable responses to various kinds of external shocks ("technology shocks"), each of which corroborate the others.

DGE models that incorporate assumptions of perfect market conditions and optimal agent responses tend to rely entirely on random ("stochastic") shocks to explain everything that actually happens. Some researchers, such as Edward C. Prescott, have sought to create simulations of an economy that replicate the behavior of the actual economy.

---

ADDITIONAL SOURCES & READING: CEPA New School of Economics, "The Neo-Walrasian General Equilibrium System"; David Colander, "Marshallian general equilibrium analysis (PDF)," Eastern Economic Review (1995);

Red typeface indicates available through JSTOR

• Sergio Rebelo, "Real Business Cycle Models: Past, Present, and Future" (PDF), Working Paper, Northwestern University (2005)
  
• Marvin Goodfriend, "The Monetary Policy Debate Since October 1979" (PDF),
  Federal Reserve Bank of St. Louis Review, (2005)
• Sergey Paltsev, "Moving from Static to Dynamic General Equilibrium Economic Models (Notes for a beginner in MPSGE)" (PDF) Joint Program on the Science and Policy of Global Change, MIT (June 2004)
  
• Jesus Fernandez-Villaverde & Juan Francisco Rubio-Ramírez, "Some Results on the Solution of the Neoclassical Growth Model" (PDF), Federal Reserve Bank of Atlanta (Dec 2003)
• Marco Del Negro & Frank Schorfheide, "Priors from General Equilibrium Models for VARs" (PDF), Federal Reserve Bank of Atlanta (July 2003)
• Morten I. Lau, Andreas Pahlke & Thomas F. Rutherford, "Modeling Economic Adjustment: A Primer in Dynamic General Equilibrium Analysis," University of Copenhagen, University of Stuttgart, University of Colorado@Boulder (1997)
  
• Federal Reserve Quarterly (Fall-1986)
  • Rodolfo E. Manuelli, "A guide to the Prescott-Summers Debate" (PDF)
  • Edward Prescott, "Theory Ahead of Business Cycle Measurement" (PDF)
  • Lawrence H. Summers, "Some Skeptical Observations"
  • Edward C. Prescott, "Response to a Skeptic" (PDF)
• Finn E. Kydland & Edward C. Prescott, "Time to Build and Aggregate Fluctuations," Econometrica (1982).
• Robert Lucas, "An Equilibrium Model of the Business Cycle," Journal of Political Economy—University of Chicago (1975)

BOOKS: David C. Colander, Post Walrasian Macroeconomics: Beyond the Dynamic Stochastic General Equilibrium Model, Cambridge University Press (2006); Stephen M. Sheffrin, Rational Expectations, 2nd Edition, Cambridge (1996); Preston Miller (editor), The Rational Expectations Revolution, MIT Press (1996);