Solow-Swan Classical Growth Theory

This is an economic model of development conceived by Robert Solow and Trevor Swan separately and concurrently. In the late 1940's and early 1950's, the Keynesian Revolution in economics was working its way through the entire field, and in pursuit of a theory of economic growth. The initial model had the logical shortcoming that, if investment fell below a certain level, the capital-output ratio would fall, causing the economy to contract further, and so on. This was incompatible with the obvious fact of the business cycle; it was referred to as a "knife-edged equilibrium," in the sense that the economy was supposed to be balanced precariously on the precise equilibrium. Another problem was that economic growth and development are confused; they are not the same.

Solow's initial project was to model the economy as consisting of two factors, labor and capital; after deducting expansion of capital growth and labor growth, Solow identified that the residual accounted for virtually all economic growth; the residual was variously identified as "total factor productivity," "technology," or "knowledge." It ought to be noted that estimating what the residual is, is a controversial business since capital (machinery, fixtures, infrastructure) is heterogeneous mix of things, and labor varies in value or payment, and one can't just add "labor + capital" and divide the gross domestic product (GDP) by that. We have an estimate of the total national pool of capital, and another for the total national supply of labor hours worked, and economists do compare the growth in the two with the growth in GDP; since GDP grows faster that the total supply of either, the difference can be attributed to better use of both labor and equipment.

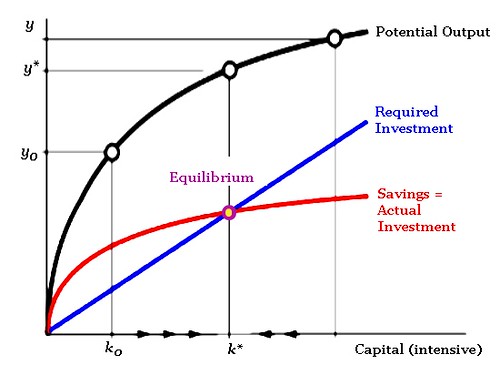
Solow's model, like Harrod-Domar's, focused on capital and labor inputs. In fact, the model is always presented intensively, so that we divide the volume of capital in the entire economy (K) by the total volume of labor (L), in order to get k. Capital k depreciates as a function of the total amount, and if the population is growing, then investment is required to keep the capital stock growing as fast as the population. The blue diagonal line in the chart indicates the correlation between k and required investment i. According to Solow's model, increasing capital produces an increase in output, but the relationship is not linear; past a certain point, increasing the capital stock will not actually increase the amount of output that each worker can consume, since it will have to be replaced so fast.


Click for larger image
While the heavy black line represents total output per worker, the red line indicates saving as a constant share of income. In the illustration above, it is true that if saving as a share of output were increased, then the economy would indeed settle at a higher rate of equilibrium consumption. (I just wanted experts to know I knew that). But with s/y at its present level, capital will necessarily settle at k*. A temporary increase in i (or ∆k/y) would increase k momentarily, but the economy would soon return to its former level of output and capital as the new capital resumed its usual rate of depreciation.

Now, the interesting thing about this model is that it was developed partly in response to, and in conformity with, the Keynesian Revolution. But it had the advantage of adapting efficiently to Neoclassical Growth Theory (PDF), and became absolutely fundamental to it. To this day, the concept of the Real Business Cycle (RBC) has remained the prevailing view in research economics; business cycles are the result of actual cycles in capital and labor inputs, accompanied by "technology shocks (abrupt changes in the Solow residual). Robert Solow was not an early supporter of RBC theory, but the concept of an economy consisting of just two inputs, plus technology, was the crucial concept. In the great majority of literature on economic research since that time, the (unattributed) Swan-Solow model is paramount.

---

ADDITIONAL SOURCES & READING: CEPA New School, "Neoclassical Growth" and "Keynesian Growth: the Cambridge Version" [Harrod-Domar Model]; Manfred Gärtner, "The Solow model" EurMacro; Bennett T. McCallum, "Neoclassical vs. Endogenous Growth Analysis: An Overview" (PDF), Carnegie Mellon University (1996)

On the Solow Residual: Yasser Abdih & Frederick Joutz, "Relating the Knowledge Production Function to Total Factor Productivity: An Endogenous Growth Puzzle" (PDF-2006) + Shekhar Aiyar & Carl-Johan Dalgaard, "Total Factor Productivity Revisited: A Dual Approach to Development Accounting" (PDF-2005), International Monetary Fund; Charlotta Groth, Maria Gutierrez-Domenech, & Sylaja Srinivasan, "Measuring total factor productivity for the United Kingdom" (PDF), Bank of England Structural Research (Spring 2004); Scott L. Baier, Gerald P. Dwyer Jr., & Robert Tamura, "How Important Are Capital and Total Factor Productivity for Economic Growth?" (PDF) Federal Reserve Bank of Atlanta (2002); Charles Steindel & Kevin J. Stiroh, "Productivity: What Is It, and Why Do We Care About It?" (PDF), Federal Reserve Bank of New York (2001);

On Real Business Cycle Theory: for a favorable treatment of RBC theory, see Sergio Rebelo, "Real Business Cycle Models: Past, Present, and Future" (PDF) Northwestern University & NBER (March 2005); a good article explaining the connection between the Solow-Swan Classical Growth Theory and RBC theory is Mark Rush's "A primer on real business cycles or the ABCs of RBCs," Business Economics (July 1990).

In order to conduct empirical work with their models, many real cycle researchers often use so-called "Solow residuals" as a proxy for technology shocks. [...] Basically, a production function relationship for aggregate GNP is assumed, say a Cobb-Douglas production function for GNP with labor and capital as inputs. Assuming that factors are paid their marginal products, data on the total shares of output going to an input can be used to infer the coefficients of the production function. Now, any change in output can be viewed as resulting from either a change in inputs or a change in technology. Using the estimated production function coefficients, it is easy to deduce what would be the change in GNP from one year to the next if only the inputs changed. Then, any difference between the actual change in GNP and this calculated change must be attributed to changes in technology.

The estimated Solow residual shocks play a crucial role in calibrating real cycle models. [...] If the basic work adequately captures the impact from changes in inputs, then any additional change in output must result from a shift in technology.