Jevon's Paradox Revisited

(Part 1)

Click for larger image Curved red lines represent different levels of "utility" (i.e., general well-being). Straight blue lines represent budget lines. Note: the utility curves are derived from a linear-expenditure model.

Utility functions are an extremely important part of economic analysis. When predicting the effects of fuel economy standards on overall fuel consumption, an economist is likely to reach Jevon's conclusions: increased efficiency will lead to increased marginal utility of consumption.

The effect of a change in prices or the shape of the utility function is to alter consumption. An increase in income will lead to an increase in the consumption of both x and y, and therefore of utility U. The shape of the utility curve determines by how much consumption of both goods goes up. Usually, when I explain the concept I set y equal to a particular good of interest, and set x equal to everything else. This is because (a) we are interested in the effect of changes in price, etc. on one particular good among many that people tend to need; and (b) the usual supply-demand curves use the y-axis to represent the price of one particular good.


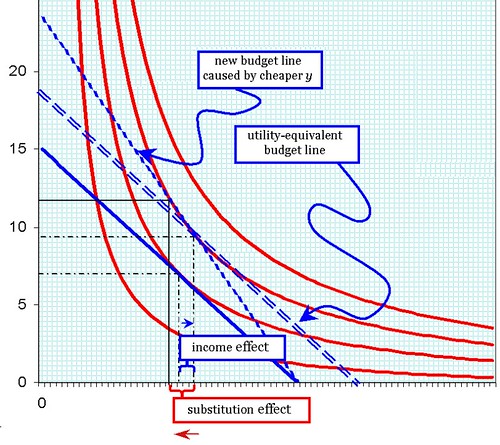
Reverting to my original analysis in part 1, we see efficiency having the exact same effect as a reduction in gasoline prices. In the chart, petrol prices have fallen 26% so you can now buy 35% more per dollar than you could before (or, conversely, engine output per unit of fuel has increased by 35%).¹ The first thing we did was plot the new (dotted) budget line, with its steeper slope. There was an increase in liters of gasoline purchased by 37% and a 1.4% reduction in the physical amount/dollar amount of everything else. Utility has increased from the second red line to the third.


Not content with this, we are still interested in the income and substitution effects caused by this. So I plotted a "utility-equivalent budget line." This is a budget line that passes through the new (higher) utility function; but it has the exact same slope as the old budget line. If the same new level of utility had been achieved as a result of an increase in income (rather than an increase in efficiency) then gas consumption would increase by only 16%, while "everything else" would increase by 8.3%. The effect of increased efficiency was that consumers substituted gasoline for other forms of consumption: gas consumption rose another 17%, while consumption of everything else fell 9%.


The significance of the two effects is not trivial. To the extent that the concepts explained above are to be taken seriously, policymakers can use taxes and subsidies to correct for perverse substitution effects. A fairly common proposal related to peak oil and ACC concerns is to restructure tax policies to offset the substitution effects caused by (say) higher CAFE standards. In other words, it would be necessary to raise gas taxes in order to pay for reductions in other taxes.

___________________________________

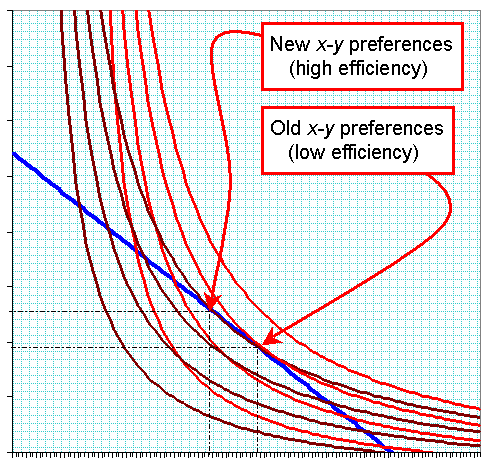This illustrates a shift from one utility function (red) to another (brown) as a result of more efficient use of y.

Returning to the 2nd approach, we used another computer model to estimate what the effect of an actual increase in efficiency would be. Part of the challenge was applying the linear-expenditure model to gasoline; the first approach merely treated efficiency as a change in budget, whereas the second treated efficiency as a change in the utility function (and hence, in differently-shaped indifference curves). Mathematically, the difference between a linear-expenditure model utility function and the more commonplace Cobb-Douglass one is that the former is actually the latter minus a constant for all values of x and y.


The graph above illustrates the shift in x-y preferences caused by increased efficiency. In the scenario I depicted, the four brown curves represent (left to right) the same four successive levels of utility as the red curves. The same budget line is is tangent to a higher "brown"indifference curve than "red" indifference curve. This time, the increase in efficiency has caused gas consumption to increase by 33% (about the same as the price decline did) but since there's no "income effect," the substitution is much larger: a 20% decline in the consumption of "everything else." Now, to clarify a point I hinted at in the previous entry: this is a bit ominous because the ratio of energy expenditures to other things has increased by a lot more than if we approximated efficiency increases by slashing the "price" of gas. In the first scenario, energy efficiency had gone up, making the dollar worth more (since more energy-intensive stuff could be bought), so the economy become somewhat more energy intensive. In the second scenario, we've faithfully replicated the changed technical conditions, with the result that the economy becomes a lot more energy intensive.


As I've mentioned as often as practical, these utility functions, graphs, and inferences are mostly arbitrary. One of many problems with the utility function, for example, is that it's long been insisted by economists that the function U(x,y) only allows you to supply a rank for different values of x and y. In order to plot these numbers at all I had to create a function in which U was a specific numerical value: 20, 30, 40... The logical implication was that 3 units of gas and 6 units of everything else, say, would produce a utility of 20, whereas if gas were increased to 8, utility would be 40. This does not mean that a 2.67-fold increase of gas consumption will make one twice as happy as before, though; it only means that one is in a position that is preferred to one in which utility = 20.


This may seem like a manageable arrangement unless we consider the thorny problem of comparing different utility functions. With a new utility function we need to compare the utility furnished by old and new bundles of goods, which cannot really coexist in time for purposes of comparison.


A more sensible handling of utility is to begin with the explanation that we aren't really measuring "well-being" in a meaningful sense, anymore than average GDP per capita measures "well-being." We are actually measuring something known more properly as "welfare," which is a rational deduction of well-being based on the ability of an economic actor to exchange or arrange what she has to achieve something nearer to her heart's desire. Welfare, another subject unto itself, could be said to capture this concept.²



_______________________________
Notes:

1 The attentive reader will notice that I'm actually saying fuel efficiency went up by 35%, which is exactly the same as the price of gas declining by 26%. We calculated that the actual amount of money spent on gas, or expenditure, went up 2%, while money spent on other stuff went down 1.4%. An implication of this is that people spent about 40% of their income on gas. This is really an exaggeration, even if we pretend "gasoline" refers to all forms of energy and include indirect purchases of energy, e.g., the share of a pizza's cost that goes towards the gas used in delivery, the natural gas used in baking it, the nitrates used in the cultivation of the wheat and tomatoes, and so on. Still, if we did account for costs like that, I think energy would account for a solid 7% of GDP.

By the way, if I had used a Cobb-Douglass utility function, then the expenditure on energy would remain entirely unchanged. This makes no sense to me: if something suddenly provides more satisfaction per dollar spent, and if you are free to do so, you will tend to spend more dollars on that thing than you did before.

2 See Partha Dasgupta, On Well-Being and Destitution, Oxford University Press (1993), p.70ff. Unusually for this blog, the link goes to a display of the actual page in Google Book where the explanation begins. Dasgupta, however, does not propose to measure well-being/welfare (W) as an alternative to utility, but as an enhanced version of it: freedom plus utility. I think this misses a splendid opportunity.

Jevon's Paradox

What happens to the consumption of a fuel, like coal or gasoline, when efficiency improves? The answer is that it goes up. This surprising answer was observed by William Stanley Jevons in 1865:

The number of tons of coal used in any branch of industry is the product of the number of separate works, and the average number of tons consumed in each. Now, if the quantity of coal used in a blast-furnace, for instance, be diminished in comparison with the yield, the profits of the trade will increase, new capital will be attracted, the price of pig-iron will fall, but the demand for it increase; and eventually the greater number of furnaces will more than make up for the diminished consumption of each. And if such is not always the result within a single branch, it must be remembered that the progress of any branch of manufacture excites a new activity in most other branches, and leads indirectly, if not directly, to increased inroads upon our seams of coal.
["Of the Economy of Fuel"]

This post will explain the concept of the Jevons Paradox in greater detail. The concept of the utility function is explained here; it's fairly handy for explaining the complexities of the Jevons Paradox.

Click for larger image

A paraphrase of the paradox is that, if the utility of anything is increased (e.g., the benefits to an individual of consuming a liter of gasoline), then the consumption of that thing increases as a share of total consumption. To illustrate, I created a chart with utility functions generated by the linear expenditure model of utility.


The first chart shows what happens if the price of gasoline declines. The vertical (y) axis illustrates the quantity of gasoline; the horizontal (x) axis represents everything else. The red lines indicate levels of well-being or satisfaction; any point along them is supposedly "indifferent," or equally, desirable. It is assumed that more of either x or y enhances one's well-being, but if one already has a large amount of (say) y, then one will be reluctant to give up a little x unless one receives a lot of y.


The blue line is the budget line. It is straight, and its slope represents the price of y in terms of x. It intersects the x-axis at the point where one spends 100% of one's income on x, and likewise with y. In the chart, the price of gasoline is lowered 26%, a decline so extreme it amounts to a sharp increase in real income. We can see the consumer responds by actually spending more on gasoline: she buys 37% more of it, and 1.4% less of everything else (the indicator lines on the chart were inserted manually).
Read more »

Utility Functions Close Up

A basic staple of microeconomics is the utility function, which is usually presented to students thus:

Let U represent consumer utility as a function of goods x and y. Maximize U(x,y) subject to I = p₁x + p₂y. U(x,y) = ln(xy).

Sometimes the textbook writer tries something fancy, like U(x,y) = α ln(x) + β ln(y), where α and β are exponents of any value.

The Lagrangian for this equation is
L(λ,x,y) = α ln(x) + β ln(y) + λ(I — p₁x — p₂y₎ And the first order conditions are
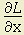= α/x — λp₁ = 0
= β/y — λp₂ = 0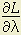
= I — p₁x — p₂y = 0

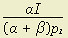These simplify to x* = and y* = , which means that expenditure on either x or y would always be exactly the same given a constant income; the actual amount consumed would vary inversely with price.

Map of Cobb-Douglas Utility function Click for larger image

Linear Expenditure Utility function Click for larger image

This is unsatisfying because the result is that there is no feedback on demand from price; demand remains unaffected by the satisfaction that a dollar spent on x yields. In real life, an increase in the price of a thing, such as energy or shelter, will cause one to consume not only less of that thing, but ultimately, seek maximization strategies in which one spends less on that thing. Most of the famous exceptions to this aren't exceptions at all; they involve an increase in income (I).


An alternative to the Cobb-Douglas Utility function is the linear expenditure function. This modifies the utility function to
U(x,y)= α ln (x - x₀) + β ln (y - y₀)
where x₀ and y₀ are given constants, and α + β = 1.

In this case, the optimal values of x*, y* are

p₁x = αI + βp₁x₀ — αp₂y₀
p₂y = βI — βp₁x₀ + αp₂y₀
which can be contrived to alter the shape of indifference curves; say, if we wanted to discuss fuel versus everything else, and then changed the subject to another type of good that is a superior good.