Xiaokai Yang & New Classical Economics (1)
Labels: economics, general equilibrium
Labels: economics, general equilibrium
(Part 1 | Part 2)
Proportional Relationships of Commodity Inputs 🙵 Outputs
By the way, we're interested here in ratios; so, for example, as inputs we have a ratio of b as 1.4 × a, and so on, whereas outputs leave a ratio of b as 1.9 × a (etc.)
In terms of outputs, (a) ≥ a, (b) ≥ b, (b) ≥ b, . . . (k) ≥ k; but notice the ratios of (a):(b):(c): . . . :(k) are quite different from the ratios a:b:c: . . . :k (Sraffa 1960, §4). An obvious corollary is that the ratios of a:(a) are not necessarily equal to b:(b), or to c:(c), and so on. The reason (a) has to equal, if not exceed, a, is that if it did not, a would have to be imported from somewhere—which would introduce a feature of the model for which no provision has been made. We could have the economy be changing relative proportions (for example, if Sraffa were interested in modelling the effects of peak oil, and a = petroleum, the annual supply of which is presumed to be declining), but for now we're not interested in that. There could be likewise be substitution (as the supply of a is less than output, somehow (b) → (k) are used to produce more of a for the following production cycle, each year. For example, (b) → (k) might collectively be used to synthesize petroleum products from coal to make up the deficit in (a). But in that case, we would treat the synthetic a as its constituents, a → k.2 It is not a problem for the realism of the model that outputs of commodities are not in the same proportion as inputs. In real life, of course, such proportions would be constantly changing somewhat, in response to depletion of some resources and new discoveries of others. Production functions would also change, and inevitably require different inputs of commodities. More significantly, though, is that all of the surplus of production over inputs is the national income. That "income" takes the form of a mix of commodities that are not required to produce next year's supply; all consumption goods are made from the national income, whether consumer durables, food, public buildings and fixtures, and so on. Plausibly the massively complex arrax of millions of different consumption goods we actually consume is derived, á la Walras, using constrained optimization, utility functions, and so forth. But it is limited by the supply of raw materials available for use. |
The relevant peculiarities, as we have just seen, can only consist in the inequality in the proportions of labour to means of production in the successive 'layers' into which a commodity and the aggregate of its means of production can be analyzed; for it is such an inequality that makes it necessary for the commodity to change in value relative to its means of production as the wage changes.The only way to avoid this problem is if we already know what the average contribution of labor is towards the production of the total national product, and find some commodity for which labor's contribution is the same as the overall average. Commodities for which labor played a larger role would (in the event of a wage reduction3) experience a comparative reduction in the cost of production. If prices in the matrix remained the same, and the values of the total amount of each commodity remained fixed, then the producers of the labor-intensive firms would be running a surplus, while those in the commodity input-intensive industries would be running a deficit (Sraffa 1960, §16).4 So we need to find an object that not only straddles the average in its direct consumption of labor, but also in its indirect consumption of labor.
Sraffa (1960), §23
Labels: economics, general equilibrium
(Part 1)
Sraffa's Production with a Surplus
Let La, Lb, Lc,... represent the labor used in the production of commodities a, b, c... and w be the wage per unit of labor; the sum of all the labors is 1, representing the total labor available for production. The production equations takes the form (Abpa + Bbpb + . . . + Kbpk)(1 + r) + Lbw = Apb . . . . . .(Akpa + Bkpb + . . . + Kkpk)(1 + r) + Lkw = Apk where r is the share of the total surplus (R) that goes to the non-labor residue—i.e, the profit. The term "total surplus" (which Sraffa calls "net product" or "national income") has a special meaning that will be explained later. Taken from Sraffa (1960), §10-11 |
Labels: economics, general equilibrium
In his book, Debunking Economics (2nd Ed), Steve Keen mentions Pierro Sraffa in connection to the dilemma of capital formation.
Walrasian General Equilibrium
The pool of available commodities is represented as a matrix of n goods and m people. People are indicated as 1, 2, 3... and goods are represented as letters a, b, c... Qa = qa, 1 + qa, 2 + qa, 3 . . . Qb = qb, 1 + qb, 2 + qb, 3 . . . Qc = qc, 1 + qc, 2 + qc, 3 . . . . . . . "Redistribution" takes place to meet the preferences of the original owners (who presumably made them in the first place). In this initial presentation of the problem, the prices of the commodities pb, pc,... are fixed (the price for commodity a is set to 1, and all other prices are in units of a). Person (1) buys x'1, y'1, z'1,... of commodities a, b, c... (this is Walras' notation, and it wasn't thought out very well!) to wind up with q'b, 1 + x'1 = qb, 1 + x'1, q'c, 1 + x'1 = qc, 1 + x'1, . . . . And Walras proceeds to demonstrate that markets will clear. Later he introduces the production process and utility functions, in a comprehensive effort to outline the system of equations the market must "solve." Chart taken from Walras (1984), p.182-184 |
Sraffa's System
Superficially differs from Walras (above) in representing production rather than redistribution (though commerce), but mathematically the concept is similar: in Sraffa, redistribution occurs because producers of wheat, iron, and pigs are exchanging quantities of those commodities in order to produce another batch of each. 90 qr wheat + 6 ton iron + 12 pigs = 21 ton iron 120 qr wheat + 3 ton iron + 30 pigs = 60 ton pigs In this example, the output is equal to the inputs, and exchange must take place again afterwards so that the same amount of everything (as before) can be produced. Subsequently, Sraffa switches to scalable matrix algebra to allow for many different commodities. Here he shows the arrangement of identities required to ensure continuous production. The term Ba prefers to the amount of commodity b used in the production of a. The amounts used in the production of each commodity are fixed by available methods and the amount of each commodity "required" by Sraffa's "economy." Aapa + Bapb + . . . + Kapk = Apa Abpa + Bbpb + . . . + Kbpk = Bpb . . . . . Akpa + Bkpb + . . . + Kkpk = Kpk When solved, the values of p ensure that the producers of each commodity will be able to buy the inputs they need in order to reproduce the output of the previous cycle. Subsequently, Sraffa develops his imaginary economy to include wages and economic surplus. Taken from Sraffa (1960), p.4 |
Labels: economics, general equilibrium
Productive Factors in DGE Economics
Labels: economics, general equilibrium, rational expectations
This is an economic model of development conceived by Robert Solow and Trevor Swan separately and concurrently. In the late 1940's and early 1950's, the Keynesian Revolution in economics was working its way through the entire field, and in pursuit of a theory of economic growth. The initial model had the logical shortcoming that, if investment fell below a certain level, the capital-output ratio would fall, causing the economy to contract further, and so on. This was incompatible with the obvious fact of the business cycle; it was referred to as a "knife-edged equilibrium," in the sense that the economy was supposed to be balanced precariously on the precise equilibrium. Another problem was that economic growth and development are confused; they are not the same.
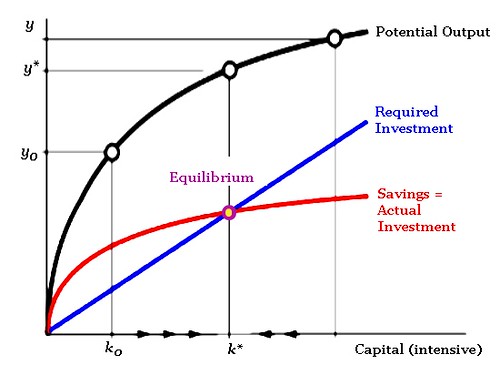
In order to conduct empirical work with their models, many real cycle researchers often use so-called "Solow residuals" as a proxy for technology shocks. [...] Basically, a production function relationship for aggregate GNP is assumed, say a Cobb-Douglas production function for GNP with labor and capital as inputs. Assuming that factors are paid their marginal products, data on the total shares of output going to an input can be used to infer the coefficients of the production function. Now, any change in output can be viewed as resulting from either a change in inputs or a change in technology. Using the estimated production function coefficients, it is easy to deduce what would be the change in GNP from one year to the next if only the inputs changed. Then, any difference between the actual change in GNP and this calculated change must be attributed to changes in technology.
The estimated Solow residual shocks play a crucial role in calibrating real cycle models. [...] If the basic work adequately captures the impact from changes in inputs, then any additional change in output must result from a shift in technology.
Labels: economics, general equilibrium, Swan-Solow Growth Theory
There is a game of chance called "St Petersburg," which is the simplest thing possible. Take a fair coin and flip it. You have bet 2 rubles on the outcome. If the coin comes up heads then you win 2 rubles, but if it comes up tails you play again, this time for 4 rubles. Each time, the stake is doubled, so n plays yields a prize of 2n rubles. Each flip of the coin is called a "trial" and the string of trials with their outcomes that concludes the game, is called a "consequence."
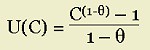

The behavioral inference drawn from this chart is that the utility of expected income U[E(z)] is greater than the expected utiliy E(U), i.e.,
The essential fact is that "risk" means in some cases a quantity susceptible of measurement, while at other times it is something distinctly not of this character; and there are far-reaching and crucial differences in the bearings of the phenomenon depending on which of the two is really present and operating. There are other ambiguities in the term "risk" as well, which will be pointed out; but this is the most important. It will appear that a measurable uncertainty, or "risk" proper, as we shall use the term, is so far different from an unmeasurable one that it is not in effect an uncertainty at all. We shall accordingly restrict the term "uncertainty" to cases of the non-quantitative type. It is this "true" uncertainty, and not risk, as has been argued, which forms the basis of a valid theory of profit and accounts for the divergence between actual and theoretical competition.
[Risk, Uncertainty, and Profit, 1921]
Labels: constant intertemporal elasticity of substitution, constant relative risk aversion, economics, general equilibrium, probability, risk, utility
(Part 1)
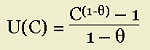

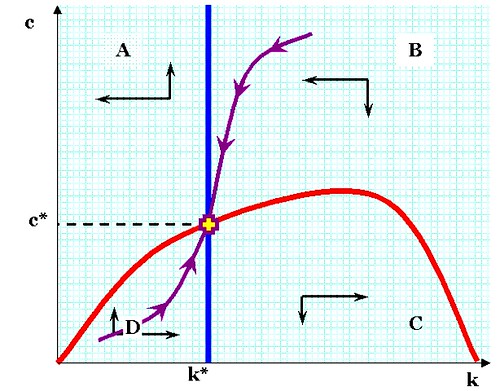
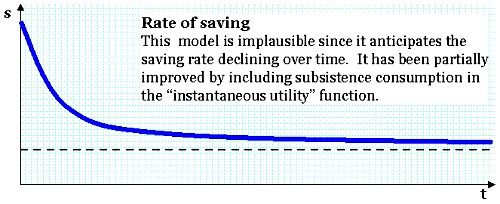
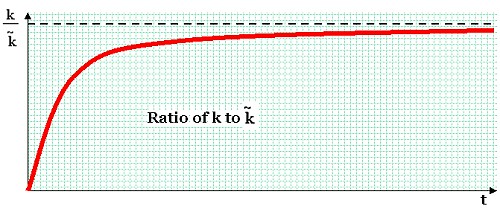

Labels: constant intertemporal elasticity of substitution, constant relative risk aversion, economics, general equilibrium, planning, Ramsey-Cass-Koopmans Model, rational expectations
Often, economic models seek to explain business decisions based on a snapshot of conditions. Hence, we have the case of the indifference curve and the production curve. Both are closely analogous:
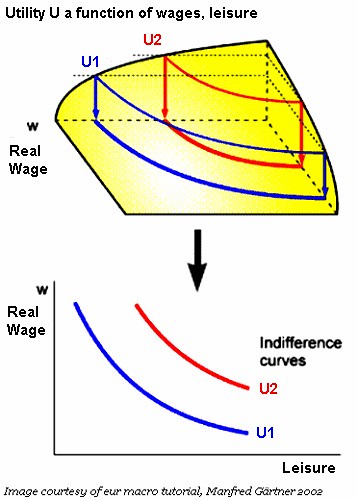
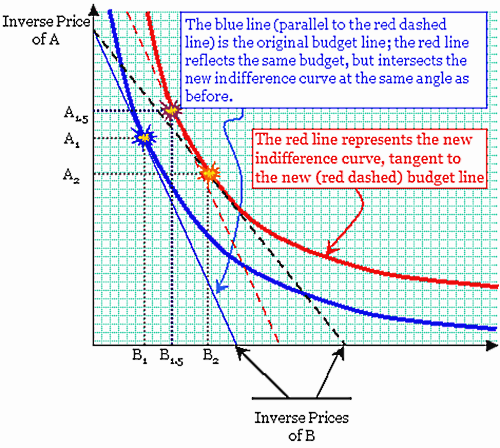
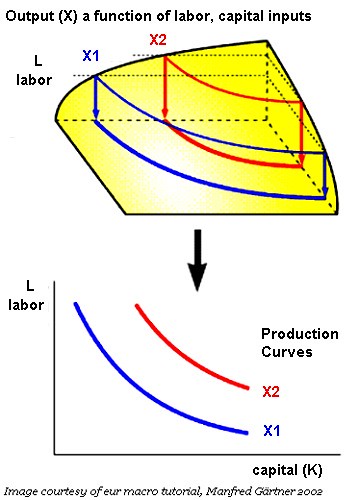
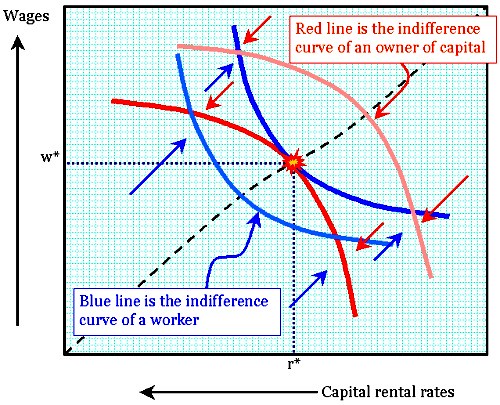
Labels: economics, general equilibrium, indifference curve, Pareto optimization, planning, utility
Readers will probably be familiar already with the fundamental economic notions of supply and demand, of diminishing marginal utility/productivity, and so on. I'm hoping readers understand the mutual compatibility of free will and the "laws" of economics, also. John Ruskin, in Unto this Last (1862) complained that economics had no room for meritorious or selfless motives; there was no room for solidarity between employers and laborers, for example.
Among the delusions which at different periods have possessed themselves of the minds of large masses of the human race, perhaps the most curious—certainly the least creditable—is the modern soi-disant science of political economy, based on the idea that an advantageous code of social action may be determined irrespectively of the influence of social affection.However, Ruskin's understanding was imperfect: non-economic, or counter-economic, motives (such as emotional affinity for one's employees) are not incompatible with the concept of labor markets per se; rather, such motives tend to average out. For example, if someone boycotts Starbucks, others may just as likely develop "consumer loyalty" to the same firm, or a "social affection" to the staff of a particular franchise. Nor is Ruskin's objection convincing in regards to the labor market: if some firm out there, such as Old Fezziwig's, pays its workers more than it absolutely must to prevent their starvation or flight, then this reduces the number of persons Old Fezziwig may employ, thus pushing the general level of wages down by a very slight amount.
No longer will economists rely on crude statistical models of how people behave in response to a policy change, such as an interest-rate rise or a tax increase. Instead, they will be able to peer directly into the brain to predict behaviour.Here, neuro-economics is used as a research tool in "behavioral economics," i.e., the study of economic decisions made by individual actors. The original study of behavioral economics employed the familiar scheme of translating the researcher's individual hypothesis about economic behavior into a constrained optimization problem, then "modeling" economic events as if the nation consisted of 300 million identical humans. It was obviously a simplification, but it could be used to screen out categorically absurd scenarios. It was Quasi-Rational Economics, by Richard Thaler and Hersh Shefrin, and it introduced such compelling ideas as the split personality ("planner-doer"). Those interested in an introduction to behavioral economics can read "Behavioral Economics" (PDF) by Sendhil Mullainathan & Richard Thaler.
First of all, what role does caudate nucleus play?The next day, in "The Consilience of Brain and Decision," Crnic reviews a paper of the same title; he outlines some of the practical principles, without spelling out how this might affect economic modeling or analysis. I really need to return to these posts and others of Crnic to understand them properly, especially since there are so many links I will need to read.
[Nature Neuroscience paper]: The human striatum has been implicated as a critical structure in trial-and-error feedback processing and reward learning. In particular, the caudate nucleus, a structure linked to learning and memory in both animals and humans has been shown to have a role in processing affective feedback with responses in this region varying according to properties such as valence and magnitude. It has been shown that activation in the human caudate nucleus is modulated as a function of trial-and-error learning with feedback.This clearly indicates that the perception of the moral character of the partner in the trust game directly influences the neural mechanisms connected with feedback processing in trial-and-error learning
Labels: economics, game theory, general equilibrium, rational expectations, risk