Knife-Edge Equilibrium

A condition in which something must either be at a precise equilibrium, or else tumble way into catastrophe. In some cases, such as something that really is balanced on a knife's edge, it's an accurate description. However, in models of (say) economic growth, it's a severe flaw in the model.

One of the most famous examples of the knife's edge equilibrium is in the Harrod-Domar Growth Model (1949), which sought to integrate some theory of economic growth with the Keynesian General Theory. Under the Harrod-Domar model, there is a precise rate of investment which is compatible with full employment.

Recall, from Keynes, that investment is one of the determinants of aggregate demand and that aggregate demand is linked to output (or aggregate supply) via the multiplier. Abstracting from all other components, we can write that, in goods market equilibrium:
Y = (1/s)I

where Y is income, I investment, s the marginal propensity to save (and thus the multiplier is 1/s). But investment, note Harrod and Domar, increases the productive capacity of an economy and that itself should change goods market equilbrium.

For "steady state" growth, in the language of Harrod-Domar, aggregate demand must grow at the same rate as the economy's output capacity grows. Now, the investment-output ratio, I/Y, can be expressed as (I/K)(K/Y). Now, I/K is the rate of capital accumulation and K/Y is the capital-output ratio (call it "v"). Thus, the rate of capital accumulation, I/K, is the rate of capacity growth (call that "g"). Thus, for steady state it must be that I/K = (dY/dt)/Y = g (i.e. the rate of capital accumulation/capacity growth, I/K, and the real rate of output growth (dY/dt)/Y, must be at the same rate, g). Thus, plugging in our terms:
I/Y = (I/K)(K/Y) = gv

But recall our goods market equilibrium term from the multiplier, i.e., Y = (1/s)I which can be rewritten I/Y = s. Thus, the condition for full employment steady-state growth is gv = s, or simply:
g = s/v
Thus, s/v is the "warranted growth rate" of output. However, Harrod and Domar originally held s and v as constants—determined by institutional structures. This gives rise to the famous Harrodian "knife-edge": if actual growth is slower than the warranted rate, then effectively we are claiming that excess capacity is being generated, i.e., the growth of an economy's productive capacity is outstripping aggregate demand growth. This excess capacity will itself induce firms to invest less—but, then, that decline in investment will itself reduce demand growth further—and thus, in the next period, even greater excess capacity is generated.

Similarly, if actual growth is faster than the warranted growth rate, then demand growth is outstripping the economy's productive capacity. Insufficient capacity implies that entrepreneurs will try to increase capacity through investment—but that that itself is a demand increase, making the shortage even more acute. With demand always one step ahead of supply, the Harrod-Domar model guarantees that unless we have demand growth and output growth at exactly the same rate, i.e., demand is growing at the warranted rate, then the economy will either grow or collapse indefinitely.

The "knife-edge", thus, means that the steady-state growth path is unstable: the only stable growth path, the "knife-edge", is where the real growth rate is equal to s/v permanently. Any slight shock that will lead real growth to deviate from this path ensures that we will not gravitate back towards that path but will rather move further away from it.

That is an unacceptable knife-edge condition, since it describes conditions that are unrealistic. But there is another case of a knife-edge equilibrium that is wide-spread and accepted in the world of economic theory: the Ramsey-Cass-Koopmans Model:


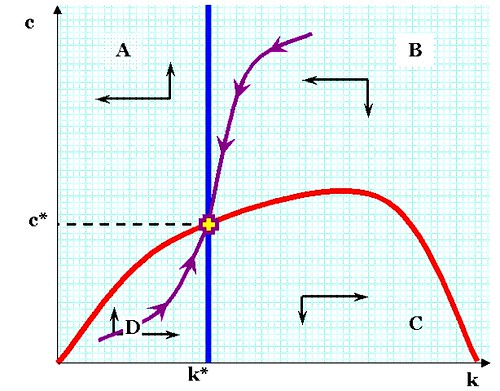
Click for larger image
In the diagram above, k refers to the level of capital per worker in the economy, and c refers to the rate of consumption (per worker). The red curve shows all the combinations of k and c that ensure a steady rate of consumption, while the vertical blue line indicates a fixed value of k*; levels of consumption that do not sustain this pool of [depreciating] capital will lead to a steady drift of k to the left, i.e., to ever-lower levels of k. If savings is too high—and consumption too low—then k will accumulate faster.

Consider the red line a bit. If k is at or about zero, then c must be very close to zero because output (y) will be infinitesimal. If k is about midway between 0 and k*, then c must be extremely small—not merely because total output will be small, but also because c/y must be small enough for k to grow faster than the population growth rate and the rate of capital depreciation. But as we reach k*, we can loosen the belt and live a little, because the rate of capital accumulation (∆k/k) only needs to match the rate of capital depreciation and population growth in order to stay the same. If k is, say, midway between k* and the far right of the graph, then capital depreciation becomes enormous, and the rate of capital replacement becomes prohibitive. Yes, k is growing but depreciation will grow even faster than y, and the rate of consumption that is consistent with steady-state growth begins to shrink. Logically, y also declines, since investment opportunities have shrunk as well. Eventually, there is some point where k is so huge that depreciation is equal to GDP.

Now look at the purple line with the arrows. Mathematically, that's the path of stable approach to the desiderata of stable consumption and stable capital stocks. At (c*, k*), capital is replaced at a rate identical to population growth plus depreciation, and y is sufficiently high that this can be done while maintaining a steady rate of consumption. And if one is on the purple line, but not at (c*, k*), then one automatically proceeds to that point. If one off the purple path, the immediate short-term effect is one moves away towards oblivion. However, there's a difference here. The chart is not fate, but a map of derivatives; it's known as a phase diagram. According to the RCK model, people are assumed to be optimizing. In other words, if you wandered off the purple path, you would immediately notice something was wrong because the slope looked really ugly, and you'd wander back. The assumption that humans are maximizing under constraints is built into the model.

(NOTE: I am not endorsing the RCK model, which is designed as an explanatory instrument anyway; I'm merely explaining the distinction between it and other forms of knife-edge equilibrium.)