The Dynamics of Industrial Choice (2)

(Part 1)

Industries make decisions about the implementation of technologies according to expected returns of that implementation: that's the standard position of orthodox economic theory. The reality is more complex, but it's interesting to see how even the very simple, reductionist mathematical models used to simulate the behavior of a simple economy lead to complex systems.

Since the basic rules of economic explanation are relatively simple, efforts have been made many times to reduce these to mathematical formulas that can describe the workings of a system. One idea has been to use these to re-create the laws of motion that prevail in an economy, so that the rules can be refined based on their predictive powers. The best-known attempt to do this has been the Ramsey-Cass-Koopmans Model, which simplifies the job by treating the economy as if it consisted of a single, average household.

The RAMSEY-CASS-KOOPMANS MODEL
Attributes of the household are inherent in the economic system. Households have endowments of labor (l) and capital (k). Labor is paid at wage w and capital commands an interest rate r. Hence, the income (y) of the household will be

y = wl + rk. However, while the endowment k accrues interest without labor, it also depreciates at rate δ; presumably r < δ, or else there would be little point in holding k. Likewise, L is accumulated from y - c; in the RCK model, all income that is not immediately consumed is saved, and therefore invested in the form of more k.

In economics, K always represents the total stock of capital; k (small) represents the supply available to our sample household at any moment in time. The symbol ρ stands for the discounting of future consumption; economists assume that consumers value future consumption less than present consumption.¹ Stocks of capital depreciate at a rate of δ, so they must be replaced at a rate of δk. There must also be a rate of return on capital, which is r; it's common to assume that r = ρ + δ, since (by definition) if r < ρ + δ, people would be irrationally postponing consumption, and if r < ρ + δ, people are irrationally improvident. Each household is intuitively driven to maximize the equation below.
This is not as far fetched as it might seem. That's because the "average" path taken by millions of households groping towards an optimal allocation may well fit this description. Groping comes in the form of endless brushes with frustration and lost opportunities. Errors or eccentric decisions made by this or that individual may be expected to average out over very large numbers and over great lengths of time.

The household stock of capital increases at rate , which will be
= (r – δ)k + wl - c
There is a consumption function U(C) is assumed to take the form below:

This is the function for constant relative risk aversion (CRRA); it is also known as the continuous intertemporal elasticity of substitution (CIES) function. Since we do not impose a time horizon, there's a risk of what is called a "corner solution," which is where the maximum point of a function lies at one limit or the other of its domain. The danger here is that the solution would be "c = 0" for all t < ∞, since ∞ is the biggest number we have. At the end of time, k_∞ would be extremely large, but the who affair would be utterly pointless since our whole effort to simulate the economy with an average household would lead to that household acting in accordance with totally arbitrary equations. Such a scenario is unreasonable; people have to consume something even when their incomes are so low they can save scarcely anything, so we have limits to the value of infinitely postponed consumption.

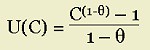
The economy also incorporates an average firm, which transforms l and k into y. Beyond this, however, the firm does not appear; it does not have an objective function to maximize, for instance; it is not in conflict with other firms or the representative household. The RCK is an extremely adaptive model, however, and a very large number of variations on it exist. Here, we'll be sticking to the plain vanilla version.



Click for larger image

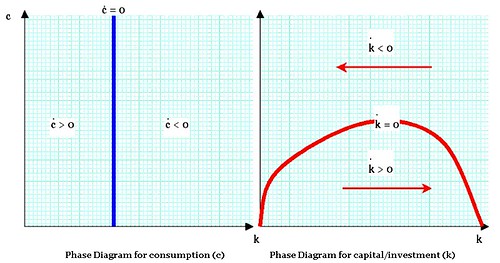
This chart shows the two phase diagrams in the RCK model. On the left, the blue line represents constant, stable rates of consumption; c-dot represents the 1st derivative of c(t) with respect to time. Let's say that k* represents the point on the horizontal axis where c-dot = 0 (where the blue line touches the bottom edge). Then levels of capital endowment k* leads to a decrease in consumption.

(Please note that c-dot is instantaneous. I point this out because, if one occupies a position {k0, c0} , then one will presently move to another point on the phase diagram.)

On the right, the red curve indicates all the positions where k-dot is 0; if one occupies positions along that line, one's net growth in capital endowments is zero. For values of c above the red line, one's rate of capital accumulation is negative (one is spending out of one's substance!). For levels of c below the red line, one's rate of capital accumulation is positive, because one is consuming so little.



Click for larger image
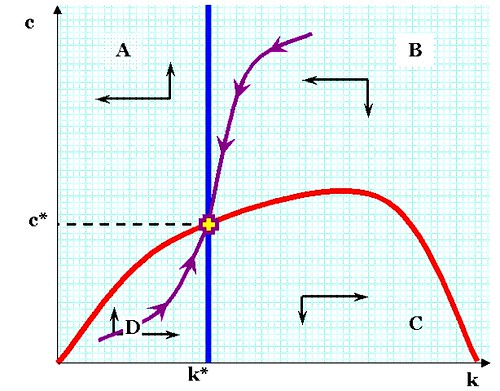
Here, the two maximization functions are combined. Where the red and blue lines intersect, there is steady state consumption and capital endowment. At points along the violet line passing through the intersection, points are not in equilibrium, but are "gravitating" towards it.

The economy (in the avatar of its representative households) is has a peculiar version of the knife-edged equilibrium. The saddle equilibrium might appear to suggest that the economy, if perturbed from perfect order, would plunge into wreckage, like a locomotive on a tightrope. Over the short-run, as during recessions, this would appear to be the case; and over very long periods of history, flourishing economies do eventually enter periods of decline. However, the RCK model pertains to medium-run trends; the model is not, nor ever could be, rich enough to capture the multifarious forces of the short-run, and over the long-run things such as civil wars, obsolete institutions, demographic changes, and so forth are simply out of the model.

The other important distinction is that when an economy is not on the violet line in the graph above, the optimization preferences of its population will tend to push it toward convergence with the steady-state, balanced growth economy. In fact, the model incorporates projections of how this occurs.


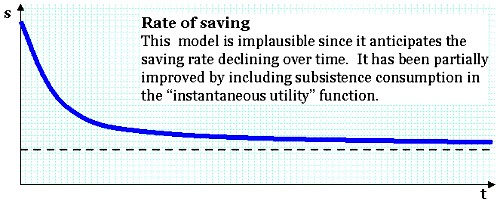
In the graph above, the economy responds with a reduction in consumption, and concomitant increase in saving. Richer models incorporate a "floor" of consumption that causes it to start low, and rise to overshoot the higher balanced growth path (BGP) savings rate.


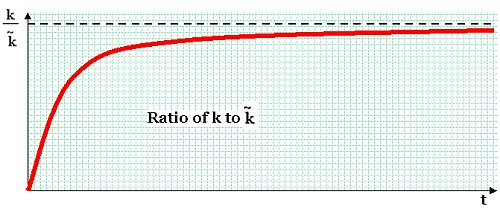
Here, the economy's stock of capital is converging. Notice that the high saving rate is accompanied by a steep slope for k; high values of s amount to exactly the same thing as high values of . Likewise, in our simplified model, the efforts of households to maximize consumption over infinite time horizons leads to rapid accumulation.


This is the big picture: the balanced growth curve, in which the endogenous factors are growing at a constant pace (dotted line) while the equilibrium growth path gradually catches up.

(Part 3)
____________________________________________
Notes

1 Time discounting: it is usually assumed that humans generally prefer consumption in the present to consumption in the future. As a result, we assume humans have to pay more to consume now than they do if they wait.  Discounting is a way of expressing this preference in the form of a low price for future consumption.

As always, special exceptions may apply but remember, economists tend to be interested in average or median behavior. Even if exceptions are very common, therefore, people with unusual time-of-consumption preferences can demand the same discount as everyone else.

Typically, for purposes of government accounting the Office of Management and Budget (OMB) uses a rate of 7%, and tests for rates of 5%-9%.
____________________________________________
Resources and Additional Reading:

The Ramsey-Cass-Koopmans model is explained formally here (and here), for those of you interested in a backup source. The first link is to the site of Prof. Thomas M. Steger in Zurich; in my opinion, his explanation is not only the best I've seen online (and the most reliable), it's also better than the one in David Romer's textbook Advanced Macroeconomics (1st edition), which is the one I was initially using. Juan Ruiz, a Spanish economist, posted lecture notes on the RCK model that are also very easy to follow.

For a detailed introduction to production functions, see Egwald Economics;