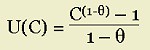The Curmudgeon's Fallacy

The belief that any preventive measure used to minimize risk of a catastrophe will be offset by increased human fecklessness. Put another way, the curmudgeon's fallacy maintains that items such as safety equipment or regulations will have almost no net impact on safety or health, since people will simply become more feckless. The curmudgeon's fallacy actually may be applied more broadly; it is not restricted to measures intended to improve safety and health. Essentially, the curmudgeon's fallacy applies to any social goal whatever.

WEAK FORM
The weak form of the curmudgeon's fallacy is (being the weak form) less of a fallacy. It holds that constraints and safety measures imposed externally (such as traffic safety laws) will have little or no net impact on safety, since people will merely assume they are protected. Similarly, people with health insurance will be more careless with their health, people with airbags will drive more carelessly, people with legal protections against fraud or false advertising will be more easily duped.

In this sense, the assumption is not so much a fallacy when it is understood as a critique of policy measures. It is valid to say that people might respond to a protective measure by being less cautious about that particular risk. In some cases, such as unwanted pregnancies, it's probably true that massively relaxed social sanctions against extramarital pregnancies have indeed increased their frequency. However, this involves a confusion of changing consequences with changing motivations. Today, few people believe extramarital pregnancies are so awful that it would be sensible to execute unwed mothers. More on that, below.


STRONG FORM
In its strong form, the curmudgeon fallacy believes measures taken by oneself to prevent a catastrophe are as futile as those imposed from outside. For example, when I was younger I used to find healthy-living enthusiasts utterly tiresome and silly, and (privately) ridiculed the fact that they were usually sickly, joyless people. After decades of living and observing, I understand that people usually take up such lifestyles, as I did, in response to specific problems: changing metabolisms, risks of heart disease, incipient obesity, and so forth. Usually, people with congenital health problems run into this concern immediately. I would wait until I looked in the mirror and gagged at what I saw.

The strong-form curmudgeon's fallacy is more related to a contempt for the illusion of effective action. Eating greasy hamburgers with a mountain of fries and a milkshake is actually a very pleasant activity; it's natural to resent the voice that tells one to switch to rice crackers and steamed asparagus. It's natural to sneer that we're all going to die anyway. However, this is another fallacy: that a result is inconsequential if it doesn't last forever. Murder merely hastens the inevitable, but we still regard it as a horrible crime. Democratic institutions are going to disintegrate into despotic ones, some day, but that doesn't mean they're worthless while they last.

More directly, the strong-form curmudgeon's fallacy maintains that self-imposed safety restraints are really a failure to accept the weak-form version of the fallacy. To illustrate this point, suppose somebody reads an article that says that using sunscreen greatly reduces the risk of skin cancer. So she starts wearing the proper SPF sunscreen whenever she's outdoors. In effect, she's acting as if there was some law that required her to do this, even though no such law exists and would be extremely difficult to enforce anyway. She's internalized the expert advice. We assume here that she will abandon alternative precautions, like avoiding exposure to direct sunshine altogether. The strong form appears to reflect a global assumption that new precautions, such as use of sunscreen or cars with airbags, does not reflect caution by the adopter, but displaces caution--even when the person taking the precaution is doing so precisely because she is cautious.

MATHEMATICAL FORM
The curmudgeon's fallacy can be expressed in the language of mathematics. Let P_d be the probability of a disaster (e.g., a fatal auto accident). P_c is the probability of a crisis occurring, such as a car accident (which may or may not be fatal); P_l is the probability of that crisis being lethal. P_d = P_c x P_l; P_d >> 1
In order to suffer a fatal car accident (P_d), one has to have been in an accident (P_c) that is lethal (P_l). Now, suppose we install airbags in cars, reducing P_l. If P_c remains the same as before, P_d will go down. According to the curmudgeon fallacy, that is absolutely out of the question. Indeed,meaning that the unintended consequence (ΔP_c/P_c) is necessarily greater than the thing affected by human will, and
it is necessarily of opposite sign.

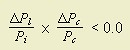
According to the curmudgeon's fallacy, it makes no difference if it is P_c or P_l that is consciously altered; if a legal measure were contrived to reduce P_c instead, causing accidents to be less likely, then accidents would become more lethal. Public policy will invariably increase P_d. At the very least, if by some miracle, the number of fatalities per passenger is demonstrably reduced, then some other awful thing must have happened.

In some cases, it is true that unintended consequences do indeed have the opposite sign and sometimes they do exceed the intended effect. Moreover, as the curmudgeon is the first to point out, there are orthogonal consequences as well. Too many regulations will interfere with each other or suppress productive activity. Safety regulations often do have perverse incentives on behavior or personal health choices. This has led to the introduction of game theory to the analysis of public policy. However, it is most rash to insist that it's always the case. This is why the expectation of large countervailing consequences is a good critique but a poor ideology.

INCIDENCE OF THE FALLACY
Typically, when conservative older men congregate, examples of the curmudgeon's fallacy tend to receive a cordial hearing. The common myth is that airbags tended to make drivers so much more careless that they offset the increment in safety (example). Of course, the authors use the example of the seatbelt:

This surprising result has triggered a number of studies, most of which have come to similar conclusions. In fact, no jurisdiction that has passed a seat belt law has shown evidence of a reduction in road accident deaths. To explore this odd but highly robust finding, experimenters asked volunteers to drive five horsepower go-karts with and without seat belts. They found that those wearing seat belts drove their karts faster. While this does not prove that car drivers do the same, it points in that direction.

A similar study was done with real drivers on public roads. When subjects who normally did not wear seat belts were asked to do so, they were observed to drive faster, followed more closely, and braked later. Statistics from the United States indicate that as more and more states required seat belt use, the percentage of drivers and passengers killed in their seat belts increased.

The cliche that seat belts save lives is true in the lab and on paper, and it's true if driver behavior does not change. But behavior does change.

Of course, if the share of motorists wearing seatbelts increases sharply, the share of motorists killed in accidents wearing seatbelts will also increase, simply because there will always be accidents that would have killed the motorist anyway. Likewise, the author cites a test that shows that motorists responded to wearing seatbelts by driving faster, braking later, and following other vehicles more closely. The author cites no actual study, which leads me to suspect the auto industry commissioned these studies (since the auto industry has long opposed any form of health or safety regulation of its products).

A careful reading of the literature reveals that the author is assuming his readers have a poor understanding of statistical inference. In order to test something like homeostatic responses to safety regulations, one has to use regression analysis with hypothesis testing to confirm or deny the null hypothesis (viz., that seatbelts have no effect on driving behavior). The study involved can then use a Wald Test on that particular null hypothesis, which means they can confirm that while safety equipment has a low predictive value on behavior, it may be part of a battery of predictive factors that do.

Yet, elsewhere, where the author cites a study (?) that fails to prove that seatbelts had a year-on-year reduction of traffic fatalities, the null hypothesis would be that seatbelt laws had no detectable effect on traffic fatalities. Since a law usually has a slow impact on behavior, this is an inevitable result. Over a period of four years, the p-value (i.e., the robustness of the coefficient) for seatbelt laws on traffic fatalities would necessarily be quite small.

However, law enforcement officials, private sector insurance carriers, and medical personnel at hospitals reliably warn motorists to wear seatbelts. From year to year, there is a distinct downward trend in traffic fatalities per passenger mile; this is slightly surprising given increases in road congestion, especially at hours late into the night. Cars have undergone numerous waves of safety-enhancing technology modifications besides seatbelts; these modifications have been adopted in many countries, reflecting agreement across ideological regimes. Additionally, there are long-term changes in attitudes about pedestrians that have nothing to do with increased motorist protection and everything to do with suburbanization of the population.

In other words, the author of the article inserted very different standards for testing behavioral homeostasis and for testing regulatory effectiveness; the standard for homeostasis could be set very low, perhaps by allowing a Wald Test; whereas, for regulatory effectiveness, the standard of rigor was markedly lower—the p-value of laws had to be less than 0.05, a nearly impossible standard in public policy research. Laws have a lagged effect on behavior, and auto safety is very complex; since any hypothesis testing may have included autocorrelation effects, dummy variables for many other explanatory variables (like jurisdictions), and a counting parameter for the passage of time, it's almost inevitable that the coefficient on seatbelt laws could be reduced to something quite small.

Finally, the essay leaves open the question, was the unintended consequence greater than the intended effect? Since the tendency has been for traffic fatalities to go down, and since private sector initiatives as well as governmental ones work the same way, it seems clear that the curmudgeon's premise has failed. Traffic regulations may have made drivers more dangerous, but the increased recklessness of modern drivers combined with greater congestion, has not sufficed to offset the aggregate effect of safety equipment and traffic regulations. Even the essay cited had to insert the weasel words, "fatality rates do not decrease as expected." They decreased, but he has some straw man out there of what was "expected" by activists.

Environmental regulations often come under attack as well; for example, using the flimsiest empirical foundations of all (the case of one [1] listed species), one of the posts at Freakonomics claims that the Endangered Species Act incentivizes property owners to destroy all of the listed specimens on their property lest development on their property be restricted. Of course, that's about all there is to Freakanomics: arguments that any public choice will have countervailing effects, QED, public choice is always bad and must be dismissed in all times and all places.

CONCLUSION: A PHILOSOPHICAL ASIDE

I never dared to be radical when young for fear it would make me conservative when old.—"Precaution," Robert Frost 1936

The curmudgeon's fallacy is that paradox of paradoxes: a precaution against precaution. A man I know well and much respect was addicted to the fallacy and used it reliably, since he was so well-endowed with natural caution and a singularly robust constitution. Once I mentioned how scandalized I was, reading Adam Smith's Wealth of Nations, about the stupendous infant mortality of 18th century Europe. He replied that he was not so sure infant mortality was such a bad thing, and insisted that I explain why I thought it was. It was a curious quirk of his character that his ideology had no part in his behavior, and he was of all men one of the most tender and generous, even though such brutal ideas flourished in his head.

At the back of the curmudgeon's fallacy is a sense that the lifelong struggle to preserve life has been a fool's errand; and in the waning years, as excellence seems to fade, there's a regret that no distinction was made between fit life and unworthy life. The curmudgeon usually lacks the will and barbarism to follow this through; but he also develops an imbalanced preference for his own "gut" prejudices over the research and formal testing of experts. At the back of this mistrust is a sense that the professional pursuit of safety, peace, and prosperity has merely spawned weakness and dependency, and that what the world really needs is a good, long epidemic to weed out the weak. As for me—I am not Lycurgus, nor was meant to be.

Constant Relative Risk Aversion

There is a game of chance called "St Petersburg," which is the simplest thing possible. Take a fair coin and flip it. You have bet 2 rubles on the outcome. If the coin comes up heads then you win 2 rubles, but if it comes up tails you play again, this time for 4 rubles. Each time, the stake is doubled, so n plays yields a prize of 2ⁿ rubles. Each flip of the coin is called a "trial" and the string of trials with their outcomes that concludes the game, is called a "consequence."

The probability of a consequence of n flips ('P(n)') is 1 divided by 2n, and the "expected payoff" of each consequence is the prize times its probability. The ‘expected value’ of the game is the sum of the expected payoffs of all the consequences. Since the expected payoff of each possible consequence is 1 ruble, and there are an infinite number of them, this sum is an infinite number of rubles. This became known as the St. Petersburg Paradox.

Bernoulli, the Swiss philosopher and mathematician, suggested the problem lay in rewarding people with money rather than utility. At the back of the paradox is the assumption that (2ⁿ)(2^-n) = 1 for all values of n; as n becomes (or could become) infinitely large, the sum of probable outcomes reaches ∞. In fact, that's not true for utility, and Bernoulli proposed that the expected utility--as opposed to expected payout in rubles--was necessarily finite.¹

Economists were increasingly interested in risk² because it applies to virtually all decisions, particularly those related to savings. Suppose you have a temporary employee working at a longterm assignment. The temp could be dismissed at any second; temps are almost never given any notice, and an abrupt dismissal typically causes the temp a lot of hardship. Because of this, the temp faces a risk if she accrues any debt; savings are vital to surviving periods between assignments. Yet there is also potential benefit in taking night school courses--say, in accounting. She must therefore weigh the risk (weighted for consequences) of dismissal, against the probability of getting a permanent job with benefits (weighted for the benefits of doing so).

Putting this another way, let U be the utility experienced by the temp. U is a function of consumption C, which of course varies over time; U = U(C(t)). The temp may prefer to take risks in order to enhance her estimated future consumption: an increase in income caused by risky investment of scarce money in tuition. For small values of θ, marginal utility diminishes more slowly--i.e., U˝(C) is smaller--than for larger values. That's the crucial significance of θ.

In the equation above, a high value of θ signifies that the consumer is quickly sated by increasing consumption. Hence, both high values of consumption all at one time, and a high payoff from a high risk bear less gratification, than would be the case if θ were low. Hence, another term for "constant relative risk aversion" is "constant intertemporal elasticity of substitution" (CIES). On average, the tendency to accept risk (in exchange for a payoff) and the tendency to accept a major belt-tightening (in exchange for a future payout) are comparable.

In the graph below, the horizontal axis C(z) refers to a random outcome; the probability that z₁ happens is p, and the probability that z₂ happens is (1-p). In other words, either z₁ or z₂ can happen. So the expected outcome E(z) is pz₁ + (1-p)z₂. Now, please notice someone has drawn a chord between points A and B. Notice that the expected utility E(U) is substantially lower than the utility of the expected outcome u[E(z)]; or just notice D and E. The position of E on the chord is dependent on the ratio of p:(p-1).

The behavioral inference drawn from this chart is that the utility of expected income U[E(z)] is greater than the expected utiliy E(U), i.e.,

U[pz₁ + (1-p)z₂] > Upz₁ + U(1-p)z₂
This is just a complicated way of saying that risk aversion inflicts a severe hit on the utility of bundle of benefits.

The function above was developed by Milton Friedman and Leonard Savage in 1948. Friedman & Savage also speculated on other shapes of the risk-utility function, but the curve above has a certain usefulness for the economics profession. You see, if a person has a curve very much unlike the one shown above, then one can be presented with a series of risks, each of which one finds acceptable, that lead one into any position; the other party--say, the casino management--can always make a profit, and essentially "pump" money out of players. While some people undoubtedly are like that, the population in the aggregate cannot be, or the economy would grind to a halt forever.

If we are looking at the function as a CIES graph, then the horizontal access merely represents increasing values of consumption. If, however, we are looking at the function as a CRRA graph, then it makes sense to regard the horizontal axis as a series of equally likely payouts. A segment between z_i and z_j with a length of 1% of the entire horizontal axis, would have a 1% possibility of happening.
__________________________________________________
NOTES

1 For those of you unfamiliar with calculus: some algebraic functions, like f(x) = x^-2 can be graphed from 0 to infinity, and the total area under their curve is finite. This seems impossible, but it's true.

2 Risk and uncertainty are (usually) regarded as distinct topics in economics. Risk is quantifiable; uncertainty is not. Or, in the words of Frank L. Knight,

The essential fact is that "risk" means in some cases a quantity susceptible of measurement, while at other times it is something distinctly not of this character; and there are far-reaching and crucial differences in the bearings of the phenomenon depending on which of the two is really present and operating. There are other ambiguities in the term "risk" as well, which will be pointed out; but this is the most important. It will appear that a measurable uncertainty, or "risk" proper, as we shall use the term, is so far different from an unmeasurable one that it is not in effect an uncertainty at all. We shall accordingly restrict the term "uncertainty" to cases of the non-quantitative type. It is this "true" uncertainty, and not risk, as has been argued, which forms the basis of a valid theory of profit and accounts for the divergence between actual and theoretical competition.
[Risk, Uncertainty, and Profit, 1921]

Some thoughts on Game Theory & Economics

Readers will probably be familiar already with the fundamental economic notions of supply and demand, of diminishing marginal utility/productivity, and so on. I'm hoping readers understand the mutual compatibility of free will and the "laws" of economics, also. John Ruskin, in Unto this Last (1862) complained that economics had no room for meritorious or selfless motives; there was no room for solidarity between employers and laborers, for example.

Among the delusions which at different periods have possessed themselves of the minds of large masses of the human race, perhaps the most curious—certainly the least creditable—is the modern soi-disant science of political economy, based on the idea that an advantageous code of social action may be determined irrespectively of the influence of social affection.

However, Ruskin's understanding was imperfect: non-economic, or counter-economic, motives (such as emotional affinity for one's employees) are not incompatible with the concept of labor markets per se; rather, such motives tend to average out. For example, if someone boycotts Starbucks, others may just as likely develop "consumer loyalty" to the same firm, or a "social affection" to the staff of a particular franchise. Nor is Ruskin's objection convincing in regards to the labor market: if some firm out there, such as Old Fezziwig's, pays its workers more than it absolutely must to prevent their starvation or flight, then this reduces the number of persons Old Fezziwig may employ, thus pushing the general level of wages down by a very slight amount.

(There are other problems with classical economics, but Ruskin doesn't really know what they are.)

Economics needs to be understood not as a deterministic prediction of how persons will behave given the prices of stuff they like, but rather, as an explanation of the tradeoffs they make. Assuming a population has a reliable set of moral virtues, for instance (like a desire to avoid polluting the environment) at a reliable concentration, a decline in the price of gasoline will still result in an increase in gasoline consumption. That's because people, however much they may dislike consuming petrol, will find a dollar spent on it to provide more utility than it did before. And even if a few diehards are determined to buy absolutely positively no more than x liters of the stuff per week, no matter what, this means that enterprises using it will still be able to buy more; indeed, if a choice exists, they might increase, say, passengers transported, by leasing more cars as cabs or express vans.

However, at the level of business institutions (including, for example, labor unions, banks, and governing bodies in the national economy), economics can make few meaningful predictions. True, the average firm will (over the greatest possible time horizon) expand production until marginal costs equal marginal revenue; but there are many reasons why a particular firm, during a particular period of operation, will not. One reason is that the firm may be a specialty producer of things like ocean-going vessels or large buildings; its production levels may be controlled entirely by the local demand for a highly-specialized product. There is no meaningful demand curve for such a business, since, even if it could cut costs and prices by two-thirds, the industry for which it produces could only consume the same number of hydrocracker units or tower cranes.

Another reason is strategic-temporal. Most firms cannot just increase output by whatever amount they need to reach MC=MR. If you are the manager of a semiconductor fabrication firm, for example, you many want to increase output by 31.5%, but a new facility will increase output by 65%. If you stay where you are, marginal costs may be quite different from marginal revenues; but if if you get the new facility, you'll be working with an entirely new set of cost and revenue curves. Even if you have reached a point where the advantages of such an expansion are totally certain, you may wish to wait until the industrial union has negotiated a new contract before announcing the new plant.

Other reasons—presumably the best-known reason—has to do with solutions of the duopoly problem. If you have only two big firms that sell a product, both will want to reach MC=MR; MR varies with the sales of the firm, so both duopolies and monopolies enjoy higher marginal revenue if sales are held artificially low. Unfortunately for the manager of the duopoly, the other firm wants you to reduce sales so it can reap the higher marginal revenue, while you will want to do the same.


A mathematician, Antoine Augustin Cournot (1801-1877), proposed that game theory offered the solution to what duopolies would sell. He used this to extrapolate the linkage between game theory (which supplied the optimal choices for individual actors) and economics (which anticipated the behavior of vast numbers of actors).

Game theory was an exotic concept for economists until the 1950's. In 1951, mathematician John Nash introduced the Nash Equilibrium (actually, the mathematical explication); then John Harsyani introduced ('58) the concept of Bayesian approaches to a Nash Equilibrium. The tremendous analytical opportunities opened by game theory and the digital computer transformed economics, as theorists sought to meld the study of individual behavior and the behavior of entire economies, to achieve something that had far more predictive power. By the 1960's, Carnegie Mellon University professor John Muth had introduced the concept of "rational expectations," which sought to represent the economy as a scalar multiple of average actors; this idea was examined in far greater detail by Edward Prescott, who also tried to restore neoclassical economics. In effect, the new economists of the 1970's expanded microeconomic analysis to cover the behavior of the entire national economy.

The evolution of game theory and economics continued to drive most research, ultimately superceding "rational expectations." Adherents of the new classical economics, after the mid-90's, tended to downplay "rational expectations" in favor of "stochasticity" and "dynamic general equilibrium" (DGE) analysis [*]. At the same time, the new Keynesian model has incorporated both DGE and stochasticity, although since it does not believe policy is ineffective, it retains the ideological rift with the likes of Prescott, et al. However, like the new classical models, there is an element of expectation. As it happens, the role of expectations applies to prices and wages, as well as to expectations of future interest rates and inflation, so the New Keynesians could retain the old concept of sticky prices (and hence, adjustment of the economy to equilibrium via quantities, rather than fluid prices).

WHO WINS THE "GAME"? NEW CLASSICAL? OR NEW KEYNESIAN?
("New classical" is an economic analysis that emerged after 1961 and became prevalent in the USA after 1978; "neoclassical" is a synthesis of "marginalism" and emerging understanding of monopoloid markets, etc.; it became prevalent from 1890 to 1936)
The impact of game theory on economics can push it in different directions. As understood by the likes of Oskar Morgenstern, Robert Barro, and Vernon Smith, game theory was employed to make the case that monetary policy would be thwarted by financial arbitrage, while social welfare programs tended to expose economically virtuous actors to blackmail by economically weak ones.
(The "economic loser" theory, in which a socially-optimal technology is blocked by an economic class whose rents are threatened by it, is discussed and refuted in this PDF file by Acemoglu & Robinson)

From the other direction, Matthew McCartey points out that the interconnectedness of behavior under game theory assures multiple equilibria—leaving the state with the obligation to ensure the one that prevails is one corresponding to social goals. Likewise, Anatol Rapoport, noted game theorist, repeatedly treated confrontation as an institution in and of itself, which guided the formation of confrontation-promoting institutions. Cooper & John, in "Coordinating Coordination Failures in Keynesian Models" (PDF-1988), which introduced the concept of "strategic complementarity" to explain involuntary unemployment. As McCartney notes, these theories place an extraordinary burden of rationality on the individual, as well as on the individuals' self-knowledge. In the face of life experience demonstrating that most individuals lack either rationality or the opportunity to make predictions that average to accuracy, both justify their assumptions by anticipating that some economic agent will identify arbitrage opportunities and capitalize on them.

But even the notion of arbitrage does not save the rational expectation. That's because a prediction only becomes an arbitrage opportunity when discovery (i.e., the event happening) proves the prediction true or false. An example is the commodity options market. We can assume the options market for crude oil captures all available information for predicting the spot price of oil on 1 June 2006. But when 6/01/06 rolls around, the inferred price (i.e., the price for which the 6-month option price-spread was most advantageous) will probably be wrong, and the fact that a lucky few will have got it right contributes nothing to technical efficiency in the oil industry. A more compelling example is the impact of Volcker's monetary supply growth targeting in 1980, which could easily have been foreseen, but was not.

However, game theory is valuable when we are trying to assess reaction to uncertainty. Moreover, as with economic theory generally, game theory is far more useful examining why institutions fail to achieve desired results. Both are effective as instruments of analysis; they are dubious as elements in positive science. Hence, the typical confusion of critics: physics allows people to make moon landings, while economics offers an ingenious tool for defending absolutely any course of action. Neither it nor game theory can be falsified by observation, whereas physics can be. The flaw in this reasoning is, of course, that while social sciences are necessary, they are quasi-legalistic: whereas a physicist or chemist is productive regardless of anyone else understanding physics or chemistry, an economist is useful only in a population of other economists. The same may be said of lawyers; a single lawyer, entrusted with unilateral power to make decisions, is not particularly likely to make good ones, and lawyers are constantly disagreeing with one another, yet (I speak in compete seriousness), a nation without lawyers is virtually ungovernable. Again, one requires a structure run by legally-trained people to administer law; but there is no such thing as a controlled experiment for ensuring a legal decision is correct.

The ability of an economist to supply useful information about system failure stems from the techniques of analysis and scrutiny that economics has developed; the ability to compare rival historical forces (such as, rising supply and rising demand for a good, which have contradictory effects on price) and establish which one is more important, the ability to render disimilar situations into comparable ones for purposes of relevant comparison, and the ability to use mathematical models to test assumptions for absurdity, are the implements that economics brings to the social sciences. Game theory does the same thing, albeit more starkly.

New-classical economists will not take well to my previous two paragraphs. A few might nod in agreement, then insist that economics is good at identifying costly frictions (such as rent control or minimum wage rates) that can prevent full employment; but beyond that, they'd have a hard time explaining why economics had anything to say after Jean-Baptiste Say and Frederic Bastiat died. The Keynesian, in contrast, would wonder where the IS-LM curve fits into "supply[ing] useful information about system failure." Economists observing the economic implosion of the late 1920's, from '37 onward largely agreed the failure of sustaining adequate demand was responsible for the calamity, and devised various proposals to defend future demand. I would observe that, when economists began conceiving social welfare programs to ensure minimal levels of demand and institutions to prevent global financial illiquidity, they were doing their jobs successfully. But when, having developed institutions to prevent fiscal and monetary failure, they assumed those institutions would always work, they made profound errors in their own field that led to another, albeit much smaller, economic crisis in the 1970's.

The crisis was caused by the economics furnishing, as they evidently surmised, an instrument to solve the problem of the business cycle. It was so powerful its use became addictive. Yet the economists largely overlook the dangers of overuse. They failed to see how the tool could be insidious. And when at last its restorative powers were exhausted, the entire profession simply recanted fiscal and monetary policy, en bloc. Since economists did not offer alternative tools to political leaders (who demanded them), the result was that quasi-automatic fiscal policy and discretionary monetary policy continued to operate.

Today game theory is moving towards offering a meta-theory, or theory about theories. The question is no longer, what is the most appropriate judgment in any particular scenario (from the perspective of an omnipotent authority), but rather, what determines how a decision will be made? Instead of announcing the optimal decision under uncertainty, there is more interest in understanding what sorts approaches will be used, and if they are strategically different. The new field of neuroeconomics seeks to adapt to utility theory without rationality. Such a version of economics, in which actors operate in a system/institution, constrained neurologically, and limited to strategic behavior under uncertainty, would leave us about as far from classical economics as it is possible to get.

UPDATE (27 January 2006): Luka Crnic (Cherishing the Mundane) posts on the "hot topic" of neuro-economics. He begins with an article in The Economist:

No longer will economists rely on crude statistical models of how people behave in response to a policy change, such as an interest-rate rise or a tax increase. Instead, they will be able to peer directly into the brain to predict behaviour.

Here, neuro-economics is used as a research tool in "behavioral economics," i.e., the study of economic decisions made by individual actors. The original study of behavioral economics employed the familiar scheme of translating the researcher's individual hypothesis about economic behavior into a constrained optimization problem, then "modeling" economic events as if the nation consisted of 300 million identical humans. It was obviously a simplification, but it could be used to screen out categorically absurd scenarios. It was Quasi-Rational Economics, by Richard Thaler and Hersh Shefrin, and it introduced such compelling ideas as the split personality ("planner-doer"). Those interested in an introduction to behavioral economics can read "Behavioral Economics" (PDF) by Sendhil Mullainathan & Richard Thaler.
My impression is that further refinements in understanding of economic behavior at the personal level would only lead to a tweaking of the constant relative risk aversion component of utility maximization functions.

In "Social Neuroscience and Neuroeconomics," Crnic outlines some of the actual research in neuro-economics, which does indeed include fMRI scans of people playing a game.

First of all, what role does caudate nucleus play?

[Nature Neuroscience paper]: The human striatum has been implicated as a critical structure in trial-and-error feedback processing and reward learning. In particular, the caudate nucleus, a structure linked to learning and memory in both animals and humans has been shown to have a role in processing affective feedback with responses in this region varying according to properties such as valence and magnitude. It has been shown that activation in the human caudate nucleus is modulated as a function of trial-and-error learning with feedback.

This clearly indicates that the perception of the moral character of the partner in the trust game directly influences the neural mechanisms connected with feedback processing in trial-and-error learning

The next day, in "The Consilience of Brain and Decision," Crnic reviews a paper of the same title; he outlines some of the practical principles, without spelling out how this might affect economic modeling or analysis. I really need to return to these posts and others of Crnic to understand them properly, especially since there are so many links I will need to read.

(cross-posted at Hobson's Choice)

---

NOTES:
Rationality: strictly defined in economics:

1. [Transitivity] If a decision maker prefers A to B and prefers B to C, then she should prefer A to C;


2. [Completeness] A decision maker is rational if she can rank all bundles of goods. If two bundles have equal rank, then that is a valid rank and the decision maker is "indifferent" to them

Some add some other attributes, such as monotonicity (i.e., if you like A more than B, then 2xA will be better than 2xB), local non-satiation (i.e., if A is a thing you like, then 2xA is better than 1xA), continuity, convexity (meaning, the marginal rate of substitution of A for B will increase as one's supply of A increases, however slightly) etc.

---

ADDITIONAL READING: Marco Antonio Guimarães Dias, "Asymmetrical Duopoly under Uncertainty: the Extended Joaquin & Buttler Model," Pontifica Universidade Católica, Rio de Janeiro, Brazil