What is VaR?
Disclaimer: the following article is not by an expert in the subject; corrections and criticisms are welcome. These are my notes as I study the subject.
VaR stands for "Value at Risk," and represents a popular mathematical expression of financial risk. From the point of view of banking regulators, VaR refers to the range of assets that the institution bears a measurable risk of losing ("taking a haircut"). The value of VaR as a metric is that it allows any pool of assets to be evaluated for aggregate risk.
Whether or not that evaluation is of any value is now a hotly debated matter.
The Basic Idea
The day-to-day movement of asset values is assumed to be stochastic.1 When we say "stochastic" we are assuming (at least at first) a "normal distribution" of outcomes, which means if you graph the daily changes in asset prices over many years, then the statistical frequency of price changes of each particular size and direction will follow a well-known pattern. In order to estimate the risk of a portfolio of assets, we therefore need to know the mean and the standard deviation of asset value changes.
When different types of assets are in the portfolio, however, there is a further question of whether or not the assets covary or not. In other words, a portfolio contains a mixture of assets that are supposed to reduce the risk of the entire portfolio losing its value at the same time. Ideally, covariance of the different assets in the portfolio is very low, so that if A drops in value suddenly, asset B or C will not. (If covariance is negative, as with a hedge, then asset B will increase in value if A declines, and vice versa).
In 1995's, JPMorganChase began selling a service called RiskMetrics, which was accumulated means, standard deviations, and covariances of different assets.2 This made it quite easy to estimate the precise risk of an asset portfolio based on past history, even if the "portfolio" was an entire financial institution. RiskMetrics coined the phrase "Value at Risk" to refer to the maximum probable value that a portfolio could lose in a week, provided it did not exceed a 5% probability worst-case scenario. For example, suppose we have a portfolio worth $1 billion. After factoring in covariance and standard deviations of asset price changes, we establish that there's a 90% chance that the value of the portfolio will remain within a range of 0.98 billion and 1.02 billion. The downside risk is $20 million could be lost. It's possible that losses could exceed $20 million, but not very probable: less than one in twenty.
While the VaR statistic for a portfolio is a single number, it has three parameters: the downside loss, the time period (1 week) and the confidence interval (95% single-tail). One way of saying this is that the VaR represents the 5th percentile scenario net outcome: 95% of outcomes will be better, and 5% will be worse; and we're measuring the net change in portfolio value.
Suppose that the log of the portfolio value is normally distributed with annual mean μ and annual standard deviation σ. The portfolio value at concluding time T is vT and σ is the standard deviation of portfolio value.3
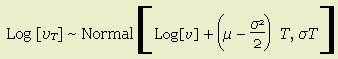
(The symbol "~" means "is equivalent to").
Most VaR calculations are not concerned with annual value at risk. The main regulatory and management concern is with loss of portfolio value over a much shorter
time period (typically several days or perhaps weeks).
The main computational challenge of VaR calculations is matrix covariance of different asset pools. Risk is increased when the different assets of a portfolio have a high rate of covariance with each other; when there is a large number of different assets held in very different quantities, then determining the covariance of all of the assets concurrently requires matrix algebra and massive amounts of historical data about prior asset movements.
Problems with VaR:
The most obvious problem with VaR is probability distribution. The distribution function used with VaR is a [log] normal distribution (the logarithm of probable asset values are supposed to be distributed normally).
The problem of computing historical asset covariance with non-normal distributions (basically, recomputing covariance from the historical data) doesn't sound like such a severe challenge, but the problem is, calculations of VaR are extremely sensitive to slight adjustments of distribution and covariance.4 While it's commonly agreed that a normal distribution is not accurate, establishing another is quite difficult.5
Another problem with VaR is that it is conceptually flawed:
I also find a real problem with the idea that one can forecast a correlation matrix.Nicholas Nassim Taleb argues:
If you try and forecast the correlation matrix, you’ve got a point estimate in the
future. The errors that we’ve seen, resulting from correlation effects, dominate the
errors in market movements at the time. So the correlation methodology for VaR
is inherently flawed.
Ron Dembo, quoted in Holton (2002), p.24
The condensation of complex factors naturally does not just affect the accuracy of the measure. Critics of VaR (including the author) argue that simplification could result in such distortions as to nullify the value of the measurement. [...] Operators are dealing with unstable parameters, unlike those of the physical sciences, and risk measurement should not just be understood to be a vague and imprecise estimate.Holton defends VaR against this criticism by claiming that all probability estimates (including covariance) are subjective.
Taleb, quoted in Holton (2002), p.24
A third criticism is that VaR permits dangerous market behavior; financial managers could package risky assets like collateralized debt securities (CDS's) as assets, and summarize pools of CDS portfolios as if they were diversified, rather than the applying covariance matrices across the entire pool of assets. In other words, slicing and repackaging mortgage obligations into securities, and reselling those securities as shares in a giant CDS portfolio, concealed the fact that covariance was basically 1 and the risk of asset devaluation was highly unstable. If housing prices were like atoms of strontium, and there was a random rate of price/isotope decay, then we could easily quantify the risk-weighted value and create a new asset with a stable value of its own. But markets for such things are not subject to ergodic probability; the risk of a generalized implosion is entirely unquantifiable.
Notes:
1 When a thing being observed, like the daily closing price of a particular stock, varies randomly, it is referred to as a "stochastic process." For a more precise description, see Thayer Watkins, "Stochastic Process" (San Jose State University, CA). There are four basic kinds of stochastic process described in the article, but we're interested in the "additive random walk." If none of these concepts are familiar, please see the link for a description.
One important distinction between random walk and stationary stochastic processes: for the latter all the shocks are transitory, whereas for random walk all shocks are permanent.
2 Aswath Damodaran, "Value at Risk"
3 Simon Benninga & Zvi Wiener, "Value-at-Risk (VaR)"
4 Tanya Styblo Beder. "VAR: Seductive but Dangerous," Financial Analysts Journal. (September / October 1995). Summary: "Applied 8 VaR calculations to 3 hypothetical portfolios. Used historical simulation with two different data bases and two holding periods (1 day and two weeks), and Monte Carlo simulation with two sets of correlation estimates and the same two holding periods. Also applied two confidence levels (95% and 99%). At the extreme, the resulting estimates of VaRs differed by up to 14 times. However, where the parameters were constrained, the differences were much less significant." Please note the probability distribution functions were not one of the parameters, but obviously if they were, then the resulting estimate of VaR would be even more different.
Glyn A. Holton, in a working paper ("History of Value-at-Risk: 1922-1998"
5 For a determined effort to do so, see Svetlana I Boyarchenko & Sergei Z Levendorskii, Non-Gaussian Merton-Black-Scholes Theory, World Scientific Publishing (2002), esp. Chapter 1.2: Regular Lévy Processes of Exponential type
Additional Sources and Reading:
Simon Benninga & Zvi Wiener, "Value-at-Risk (VaR)"
Glyn A. Holton, "History of Value-at-Risk: 1922-1998"
Thomas Linsmeier & Neil Pearson, "Risk Measurement: an Introduction to Value at Risk"
Joe Nocera, "Risk Mismanagement" NY Times Magazine (4 Jan 2004; via Kevin Drum)
Yves Smith, "Woefully Misleading Piece on Value at Risk in New York Times," Naked Capitalism (4 Jan 2004; via comment at Kevin Drum)



0 Comments:
Post a Comment
<< Home