Solving a Three-Good Utility Function
According to the principles of Neoclassical economics, we would turn to a utility function of three variables to investigate.1 Usually, the concept is explained with two goods so it can be illustrated (x and y being goods, and z—the vertical axis—standing for utility). But we can't illustrate this one fully because we are interested in cases where there are actually more than two goods determining utility.
Let U be utility as a function of x, y, and z, where x refers to everything one buys other than software, y is cheap software, and z is costly software (α, β, and γ are arbitrary constants; x0, y0, and z0 are threshold levels of consumption) .
U(x, y, z) = αln(x-x0) + βln(y-y0)+ γln(z-z0)
subject to
I = pxx + pyy + pzz .
where I is income and p refers to the price of the respective good.
The Lagrangian will be
L = αln(x-x0) + βln(y-y0)+ γln(z-z0) + λ(I - pxx - pyy - pzz)
and first order conditions will be
First we solve for x, y, and z in terms of the constants (and λ)
and then we solve for the Lagrangian multiplier λ:
And we substitute the values for x, y, and z into the equation for the Lagrangian multiplier.
Now, so far this has just been a generic solution of a symmetric 3-good constrained optimization problem, and it can be made even more general for a very large number of goods:
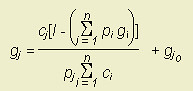
where gj is any good, cj is the corresponding constant I've been representing with Greek letters, I is income, and i is the counter for summation within the equation (So, for example, pj refers to the price for the good gj whose optimal amount g* you're trying to determine, while pigi refers to the amount expended on any individual good listed in the summation from 1 to n goods).
(Discussion of Findings)Notes:
1 Regarding the utility function: I prefer to use the linear expenditure model instead of the Cobb-Douglas model everyone else uses, because the CD utility function leads to rigid expenditures between x, y, and z. If a researcher wanted to perform regression analysis of "observed preferences" to establish what the coefficients were, the existence of threshold levels of consumption would correspond to y-intercepts for each good.



0 Comments:
Post a Comment
<< Home